中3数学 中3数学式による説明(整数の証明のポイントと練習問題) /5/13中3数学 スポンサーリンク 全国の県立・公立入試において、論理的に体系的に、答えを導けているかを確かめるために、求めるまでの過程を書かせる問題が増え、その配点も増加傾向にあります。 特に、福岡県では、大問3の数の表明や資料の整理に代表される求めるまでの過程、大問5定期テスト数学対策 中3分野 「平方根」を以下のように訂正しました。 ⑧総合演習 大問1(3)の問題文の語尾に「ただし,a>0とする。」を追加しました。 定期テスト数学対策 中3分野 「平方根」を以下のように訂正しました。 平行四辺形の証明問題 平行四辺形の性質を使った証明の練習問題です。 平行四辺形の性質をしっかり理解してから解くようにしましょう。 また合同な三角形、平行線の錯角、同位角の性質などを利用して証明する問題が多いです。
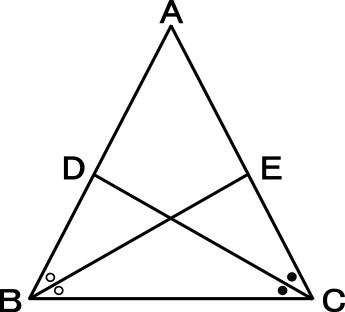
中学2年数学練習問題 図形と合同 三角形の合同の証明問題
中3 数学 因数分解 証明 問題
中3 数学 因数分解 証明 問題- 中3数学平方根の整数部分と小数部分のポイントと練習問題 整数部分と小数部分の問題 平方根を利用の問題で、整数部分と小数部分の問題は、大きく差が出る問題となります。やり方を知っている知らないかだけ 記事を読む (n1)n(n1)=3n nは整数だから3nは3の倍数 よって 連続する3つの整数の和が3の倍数になる 練習問題をダウンロードする 画像をクリックするとPDFファイルをダウンロードできます。 式による証明1 式による証明2 式による証明3
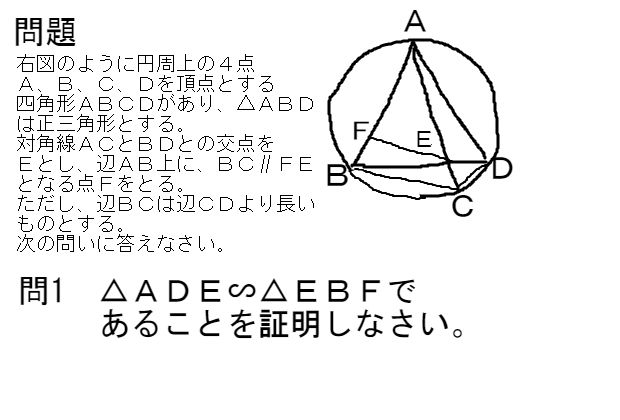



超難問入試 円と三角形 証明と求積問題 中学数学 理科 寺子屋塾の復習サイト
国際数学オリンピック(imo)の過去問の中でも,完答者が極めて少ない超難問を3問紹介します。 ・マスターデーモン(整数問題) ・世紀最難問(幾何不等式) ・過去問の中で最難問だった(組合せ) 3問とも解説が大変なので解答はつけていません。 学年 中学3年生, 教科書 未来へひろがる数学3 啓林館, 単元 図形と相似, キーワード 相似 中3 数学 相似の証明問題 9 8 0 このノートについて新編 新しい数学3 単元/教材 コンテンツ 1章多項式(教科書p8) ドミノ倒し 1章多項式(教科書p21) 因数分解パズル 1章多項式(教科書p33) 解説動画(章の問題A6前編)
7 3年2乗に比例する関数総合問題4 5問題 点a, p, qを頂点とする(誤)→点d, p, qを頂点とする(正) 3年2次方程式総合問題lv2 2(2)①と②の答が逆になっていたので訂正しました。 19/9/4 3年円周角6 ⑥答127°(誤)→ 117°(正) 証明問題はパターンが少ないので、慣れれば実は簡単です。 覚えておくべき条件が少ない! 中学数学の証明問題をクリアするには、合同な三角形の性質以外に以下の性質・条件を覚えておけば十分です。 平行線の性質; 式による証明の新傾向の問題 問題下記の<規則>に従ったxyzの値が奇数を2乗した数になることを証明せよ。 ただし、「ある自然数をnとすると」から書き出しなさい。 <規則> ある自然数nを2乗した数をx ある自然数nより1だけ大きい自然数を2乗した数をy nとn1の積を2倍した数をzとする 式による証明の新傾向の問題解答 ある自然数をnとすると、x=n2、y=(n1)2
FdData 中間期末:中学数学3 年:相似 相似な図形/三角形の相似条件/相似の証明:2 辺の比とその間の角/2 組の角が等しい/ 直角三角形など /三角形の相似と長さ/FdData 中間期末製品版のご合同の証明1 1 右の図でAC=BD、AD=BCのとき ABC≡ BADとなることを証明せよ。 2 右の図で、AB//DC, AB=DCならば、 ABO≡ DCOとなることを証明せよ。 3 AB=AC, AD=AEのとき テーマ: 実力テスト数学 リロード推奨 ~高校入試までの流れ~ 2月3学期期末テスト 3月中2学年末試験 4月第1回実力テスト (1年の範囲) 5月1学期中間テスト,第2回実力テスト(2年の範囲) 6月期末テスト 7月第3回実力テスト (1,2年の範囲)




中学数学の図形の合同の証明の問題です 2 がわからないのでわかる人いますか Clear




中二 数学 直角三角形の合同 この証明問題の の意味がわかりません W Clear
中学2年生 数学 四分位数・四分位範囲と箱ひげ図 練習問題プリント 無料ダウンロード・印刷 四分位範囲や箱ひげ図を用いることにより、複数の集団のデータの分布の傾向を比較して読み取り、批判的に考察して判断する力を養う練習問題プリントです。中学数学の問題ソフト無料 中1数学 正負の数,文字と式,1次方程式,比例・反比例,平面図形,空間図形,資料の活用 中2数学 式の計算,連立方程式,1次関数,図形の性質,確率 中3数学 式の計算,平方根,2次方程式,2次関数,相似な図形,円周角,三平方の定理,標本※ 桜中3年生の皆さん,今年も事前に過去のテストを解いておきましょう! 夢や目標は,あきらめなければ,必ずかないます! 本気なら,即実行です! <新作テスト問題> h現在 問題132本 解答 84本 (合計216本)



1




三角形の合同条件を使った証明問題 中学2年生の問題を解こう 身勝手な主張
中学校 数学3年1章18 S=alの問題を解けるようになろう。 中学校 数学3年2章3 数を根号をつけて表すことができるようになろう。 (15) 2年ー3章ー一次関数 (16) 2年ー4章ー図形の調べ方 (14) 2年ー5章ー図形の性質と証明 (9)問題一括 (10,051Kb) 解答一括 (11,805Kb) 多項式と単項式の乗除(2) 多項式と単項式の乗除(3) 多項式と単項式の乗除(4) 式の展開(1) 式の展開(2) 式の展開(3) (xa)(xb)の公式(1) (xa)(xb)の公式(2) (xa)(xb)の公式(3) 平方の公式(1) 平方の公式(2) 和と差の積の公式(1) 和と差の積の公式(2) 証明問題では辺や角が等しいと言うときにその理由を書く必要があります。この動画ではよく使われる理由を7パターン説明しています。これらを使いこなせるようになるだけで、ほとんどの証明問題は完答できるはずです。 ⭐️⭐️⭐️マイスタイル からのお知らせ⭐️⭐️⭐️ ・集




無料 中3数学 発展 応用問題 問題プリント 310 平方根2 大小
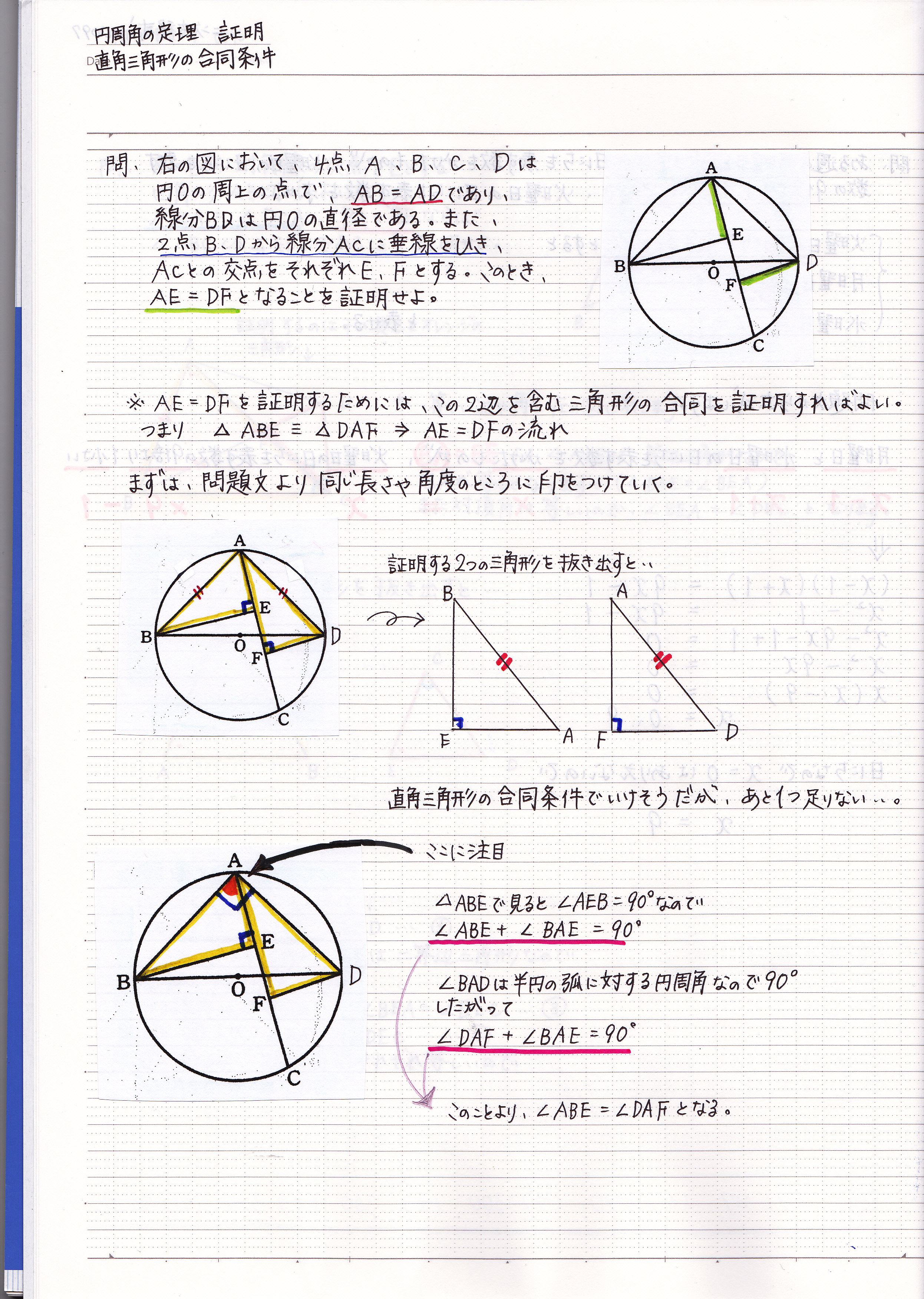



直角三角形の合同条件を使った証明問題の解き方 現役塾講師のわかりやすい中学数学の解き方
勉強法 数学 苦手な人が多い図形の証明問題を解くコツを解説! 事件現場は被害者の自宅だった。安易に家の中 因数分解のやり方を例題と共に分かりやすく解説!2乗・3乗・たすき掛けの問題を解く文字を使って、式をつくり、計算を進めればいいんだね。 証明するのは、 「連続する奇数の積に1をたした数は4の倍数になる」 だから、この部分を式にしよう。 (奇数)×(奇数)+1=(4の倍数) だね。 連続する奇数は、いま2n-1、2n+1とおいているから、 (奇数)×(奇数)+1 =(2n-1)(2n+1)+1 =4n 2 -1+1 = 4n 2If playback doesn't begin shortly, try restarting your device Videos you watch may be added to the TV's watch history and influence TV recommendations To avoid this, cancel and sign in to



カレンダーの数字の証明問題です 中3 図の中の 15 16 22 Yahoo 知恵袋
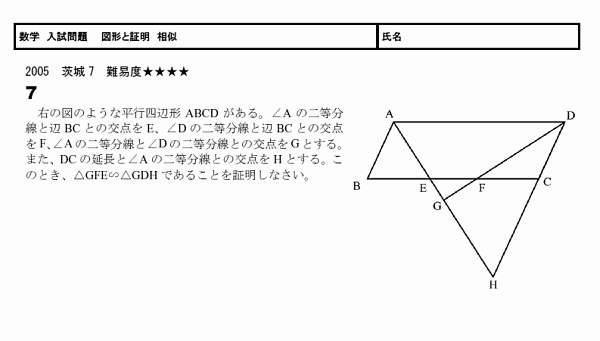



図形と証明 相似 無料学習プリント教材
このことを証明しなさい。 練習問題2 連続する2つの奇数の積に1をたすと、その2つの奇数の間の偶数の2乗になる。 このことを証明しなさい。 練習問題3 連続する3つの自然数の真ん中の数の2乗から1をひくと、その他の2つの数の積になる。結論を書いていこう。 いま結論で証明したいのは 「偶数と奇数の和は奇数になる」 だね。 (偶数)+(奇数)= 2(m+n)-1 だったから、 2(m+n)-1が奇数であればいい わけだね。 すると、m+nは整数だから、2(m+n)-1=2×(整数)-1=(奇数)となって、 きちんと 「偶数と奇数の和は奇数になる」 ことが証明できるわけだね。 証明の解答例2年生 5 図形の性質と証明 数学的な思考力・判断力・表現力をはぐくむ問題 年 組 号氏名 全国学力・学習状況調査 B問題③ 3 大貴さんは,次の問題を考えています。h21 次の(1)から(3)までの各問いに



1
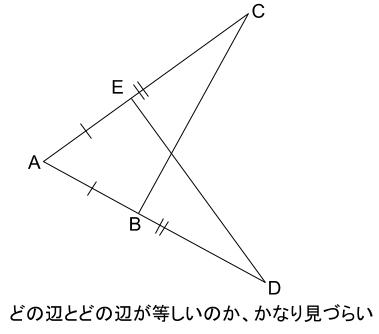



中学数学 三角形の合同の証明 その2 中学数学の無料オンライン学習サイトchu Su
今回は中3で学習する式の計算の利用から 「円、正方形の図形に関する証明」 を解説していきます。 取り上げるのは、こういった図形の問題です。2次方程式、平方根の応用、9点、問3:作図3点、問4:資料の整理、 問5:確率、問6:規則性の問題、問7:体積、問8:2次方程式の活用、 問9:2次関数の変域、変化の割合、活用、問10:相似証明、面積と 毎年出題傾向は決まっています。 これらの出題傾向 中3数学 式の計算の利用(数に関する証明)まとめと問題 入試問題でもよく出題される「式の計算の利用」、その中でも数に関する証明問題について今回取り上げました。 「2つの連続する偶数が」「3つの連続する数を」「2つの奇数の積から」などいろんなパターンがありますが、どのように式を立てたら良いかわからなくなる、と混乱しやすいところです




中3数学 道路の面積を求める問題 例題編 映像授業のtry It トライイット
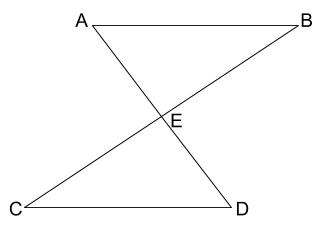



中学数学 三角形の合同の証明 その1 中学数学の無料オンライン学習サイトchu Su
平面図形 3辺から等しい距離にある点の求め方 平面図形 円の中心を求める作図 平面図形 円周角と中心角について 平面図形 証明問題の勉強法 平面図形 30゚ の角の作図について 平面図形 平行四辺形は線対称ではないのか?校数学では,証明は高等学校の幾何の指導内容とされ ていました。中学校の数学では,図形の性質の学習に おいて,性質の成り立つわけを「説明」する内容が3 年生にありました。 「証明」という用語が,戦後の中学校の教科書に登 場したのは,昭和30中学3年生 数学 2次方程式 練習問題プリント 無料ダウンロード・印刷 2次方程式の考え方と解き方の練習問題プリントです。 方程式の形に応じて、適切な解き方が出来るよう、「因数分解」「平方根の考え方」「解の公式」をそれぞれ使った3種類の方法を詳しく解説しました。
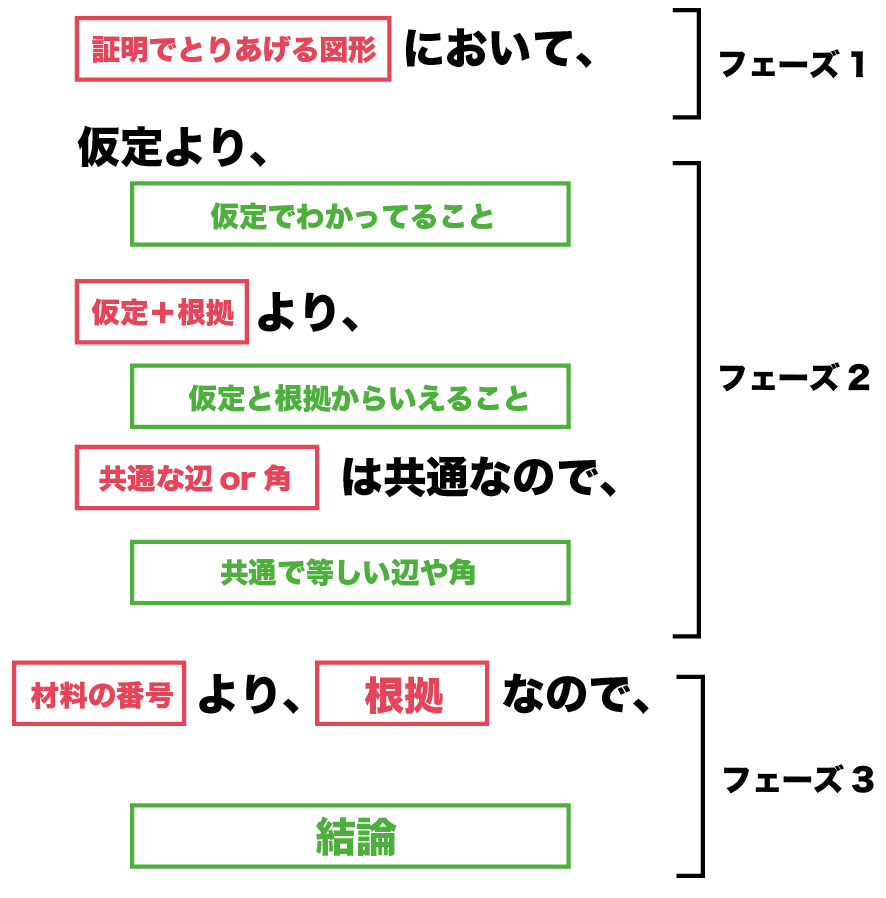



中学数学 3年間つかえる証明問題の書き方 Qikeru 学びを楽しくわかりやすく




中学2年生 数学 合同と証明 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
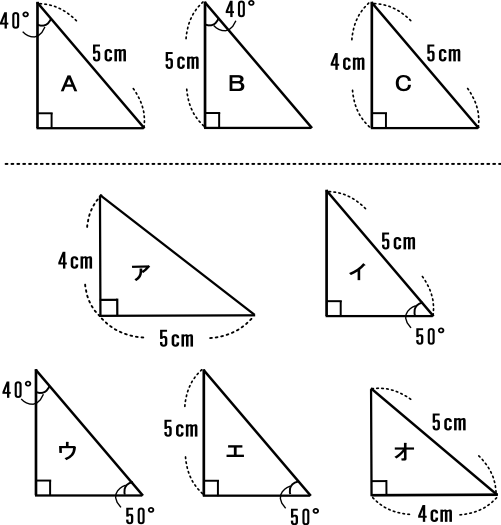



中学2年数学練習問題 直角三角形の合同条件と証明問題 図形と合同




世界一わかりやすい数学問題集中2 5章 図形の性質と証明
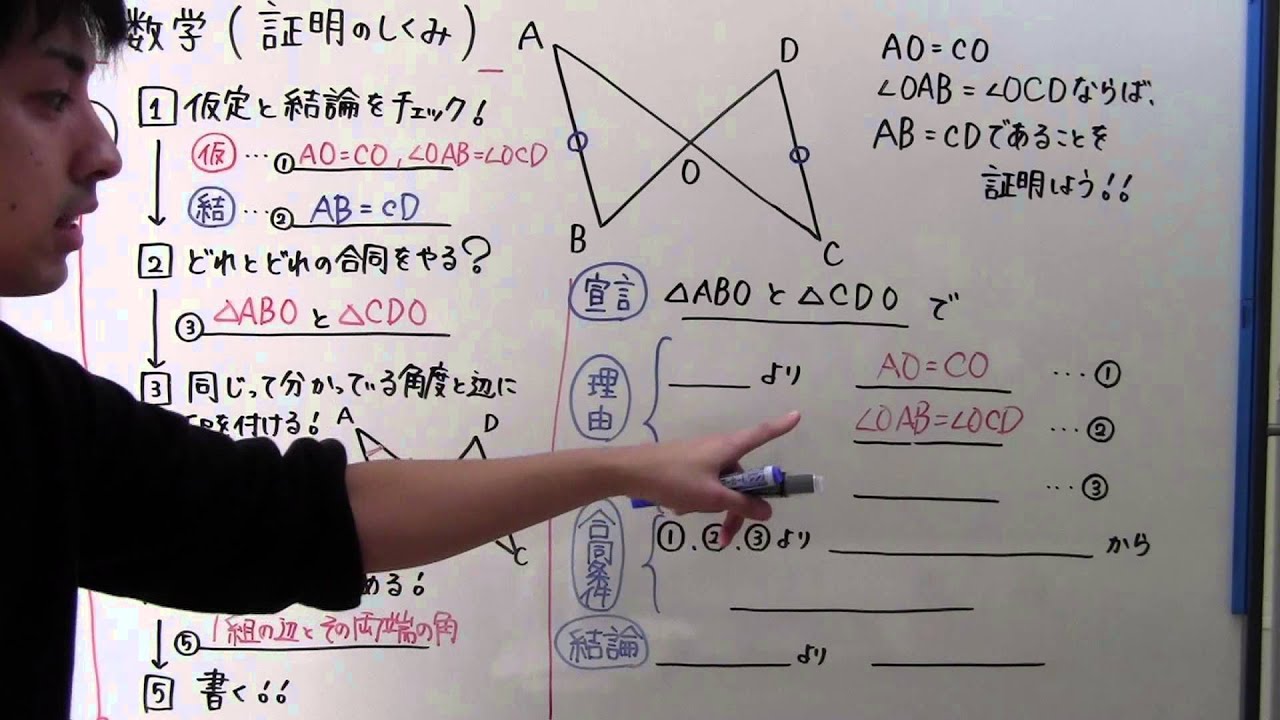



中2 数学 中2 60 証明のしくみ Youtube




中学3年 数学 東京書籍 新しい数学 相似な図形 平行線と比 赤城 ᐡᐤᐡ




中学数学 図形の証明がらくらく解ける 中学数学らくらく解ける シリーズ 学研教育出版 本 通販 Amazon
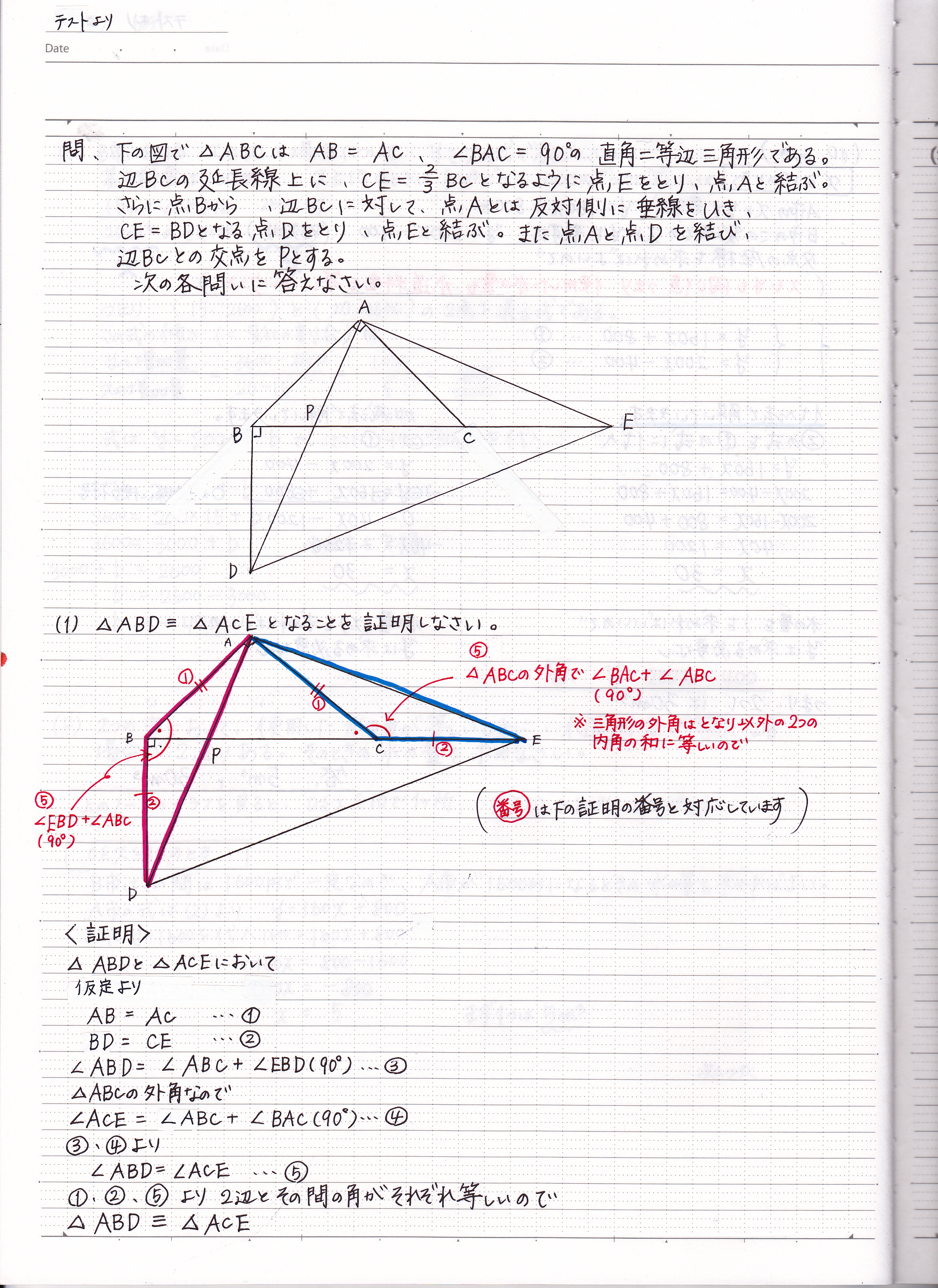



図形の総合問題の解き方 合同証明 三平方の定理 相似など 現役塾講師のわかりやすい中学数学の解き方



中3数学 式の利用 整数の証明問題の定期テスト対策予想問題 Atstudier
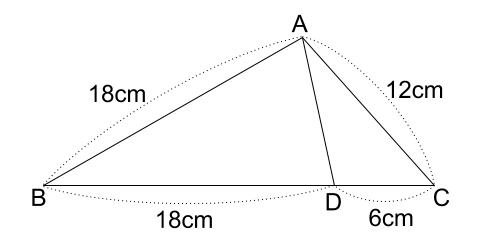



中学数学 相似の証明 その1 中学数学の無料オンライン学習サイトchu Su




中3数学 円の性質と証明 練習編 映像授業のtry It トライイット
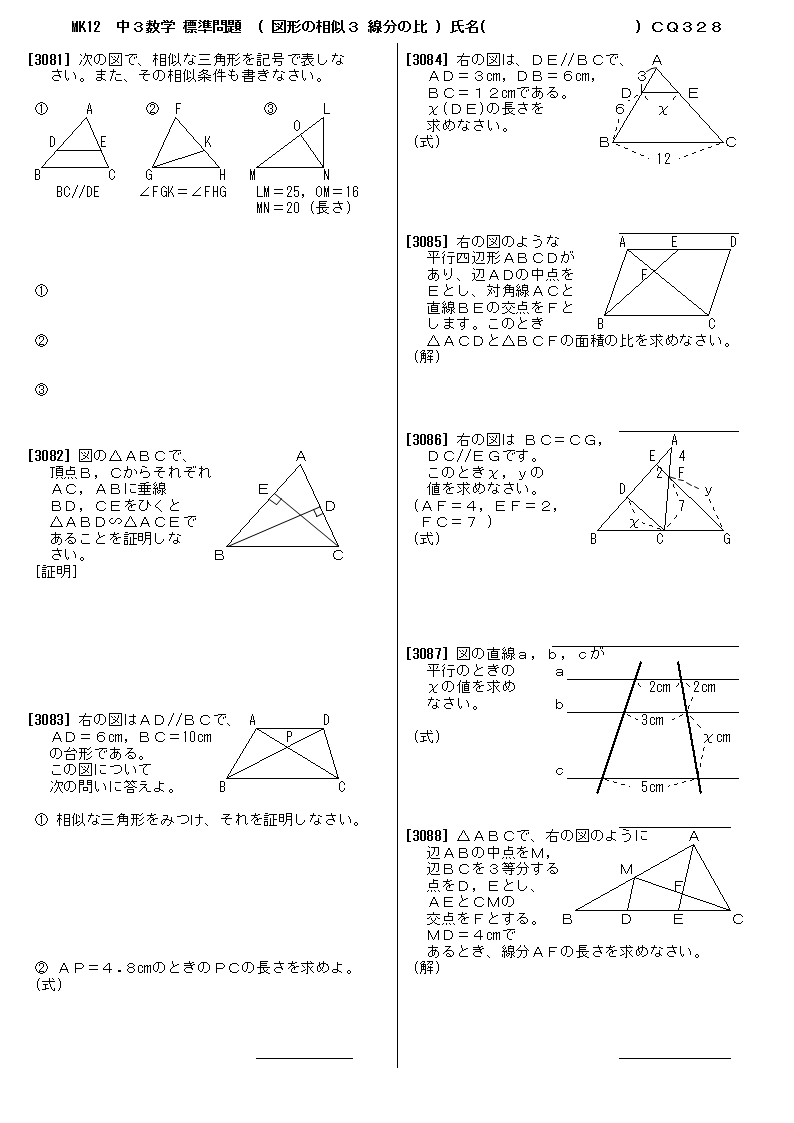



無料 中3数学 標準問題 問題プリント 328 図形の相似3 線分の比




中学3年 数学 式の計算の応用問題 Youtube




中学3年 数学 東京書籍 新しい数学 相似な図形 平行線と比 赤城 ᐡᐤᐡ
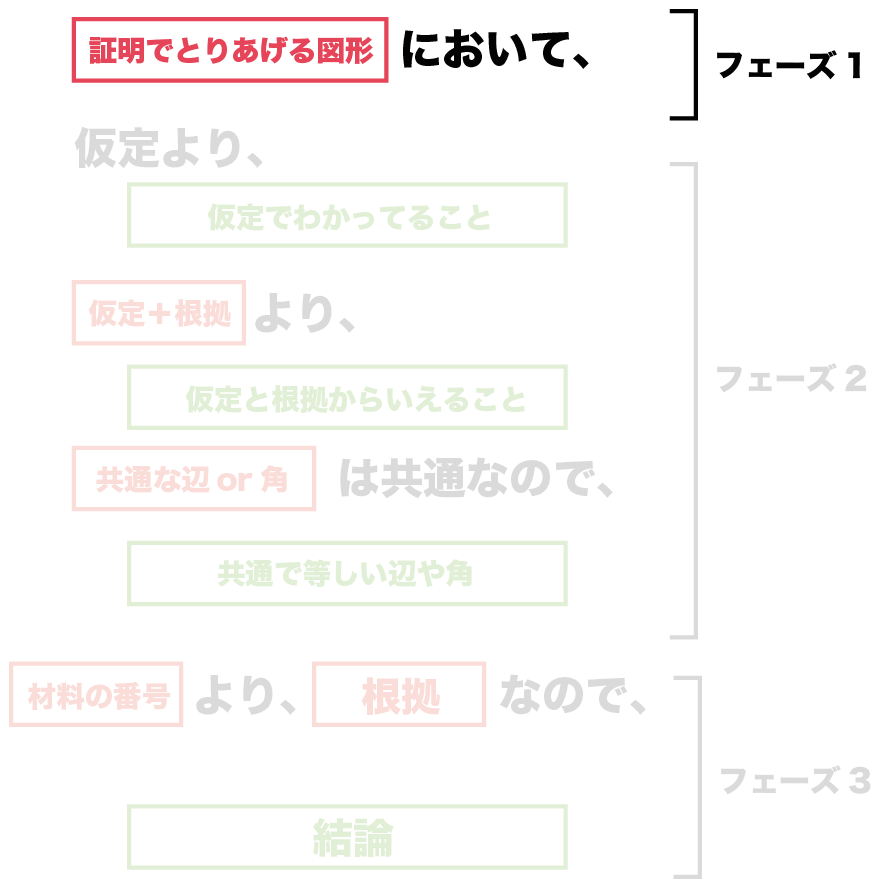



中学数学 3年間つかえる証明問題の書き方 Qikeru 学びを楽しくわかりやすく
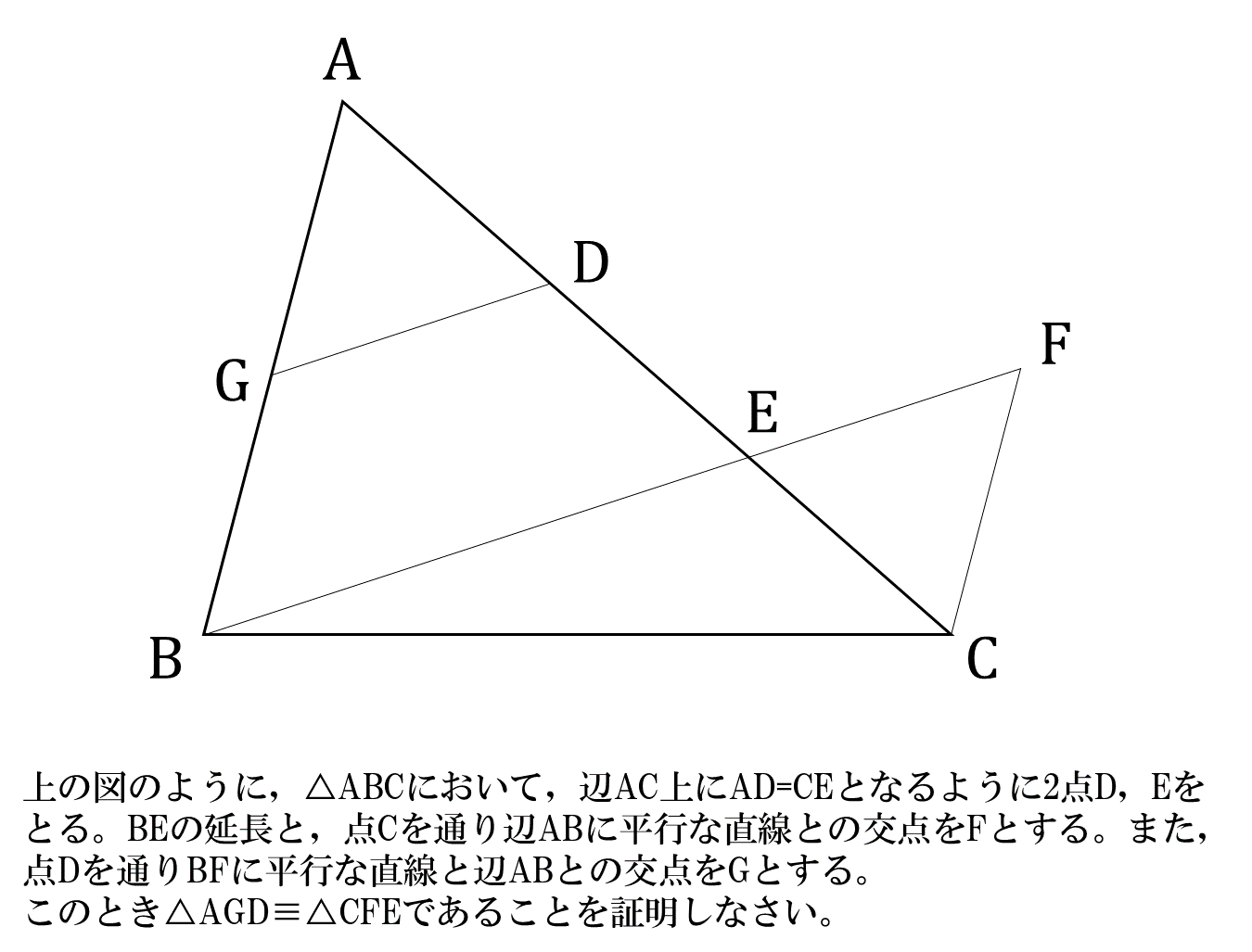



数学 中学証明問題を解く4つのポイント




超難問入試 円と三角形 証明と求積問題 中学数学 理科 寺子屋塾の復習サイト




初投稿です 中3 啓林館 P 125 相似条件と証明 練習問題 Clear




こういう難しいタイプの記述は答えを見れば あ まあ証明できてるのか ぐらいの理解がで Clear
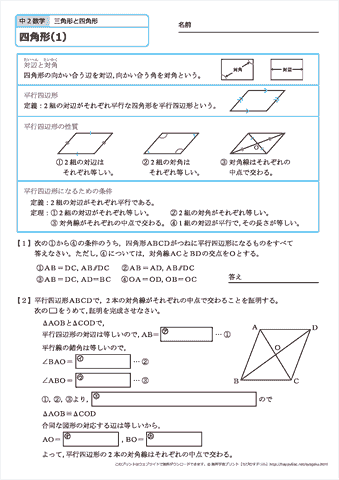



中学2年生 数学 四角形 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
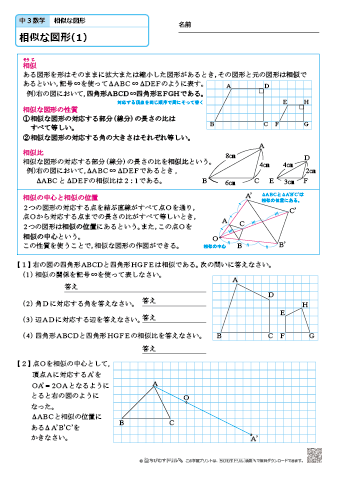



中学3年生 数学 相似な図形 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
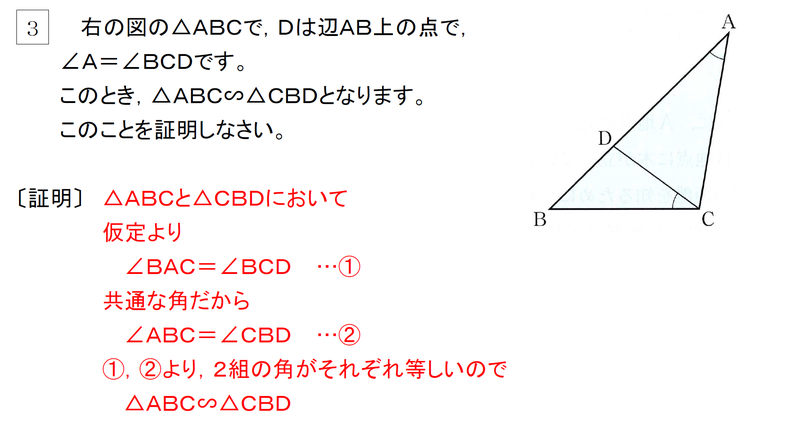



中学3年 数学 東京書籍 新しい数学 相似な図形 平行線と比 赤城 ᐡᐤᐡ
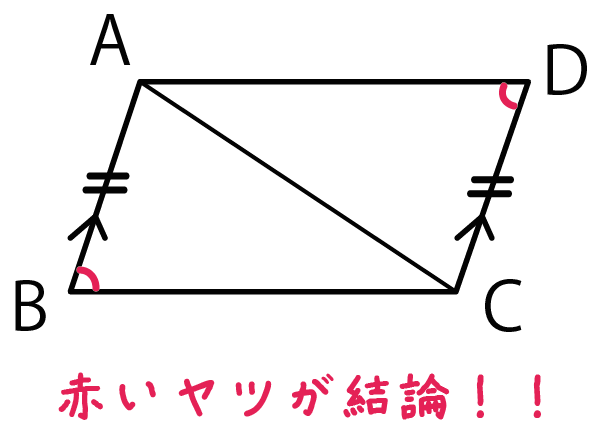



数学の証明問題の解き方がわかる4つのステップ Qikeru 学びを楽しくわかりやすく



中3数学 相似の証明のポイントと練習問題




中学2年数学練習問題 図形と合同 三角形の合同の証明問題




数学 中3 13 式の計算の利用 数字の証明編 Youtube



中学 数学の証明問題です 超難問 1 から全然わかりません 今まで見た中 Yahoo 知恵袋




この証明問題の答えの 仮説 Clear
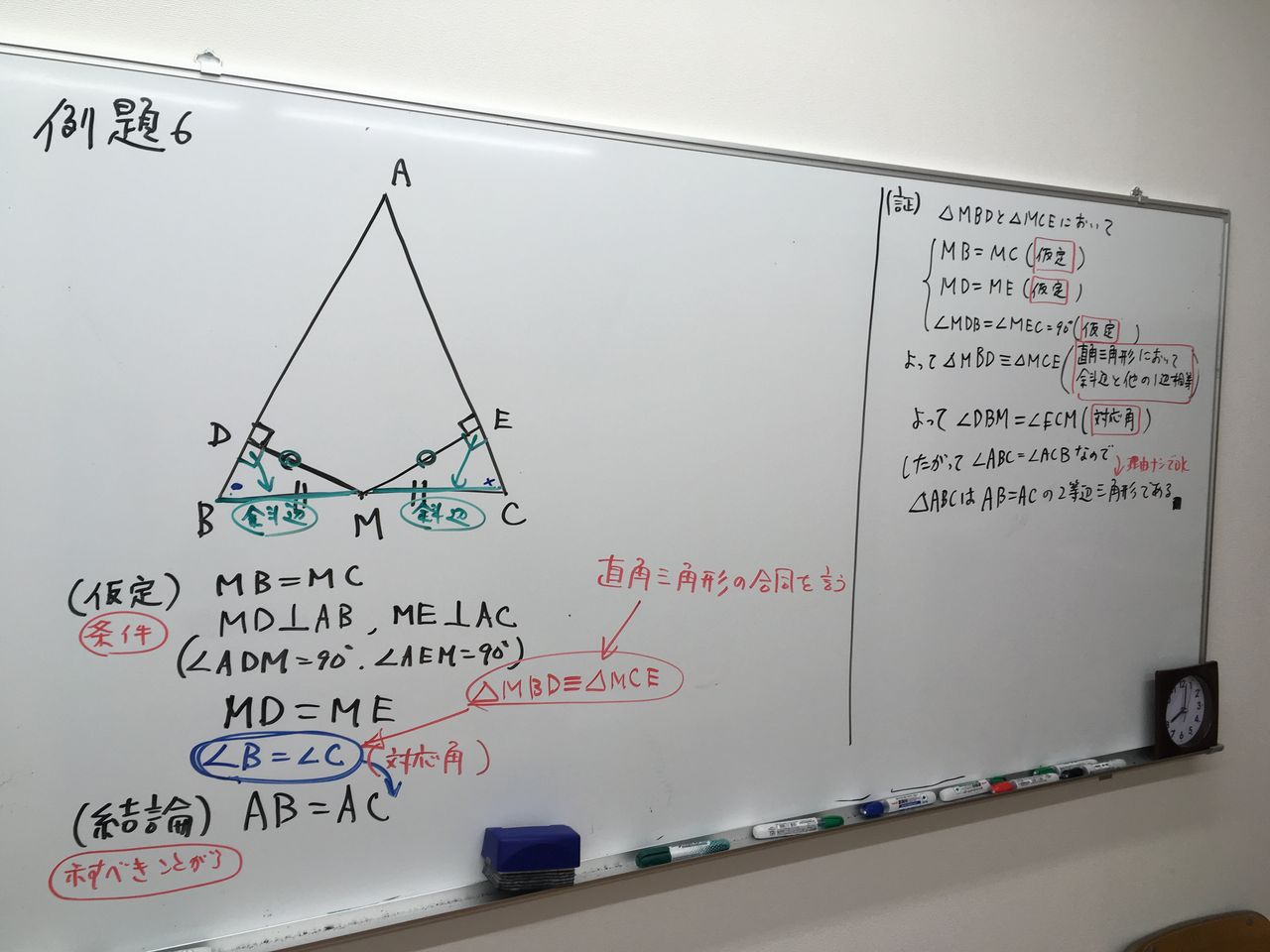



証明の書き方の作法を身につける 思考研のブログです




世界一わかりやすい数学問題集中2 4章 平行と合同と証明
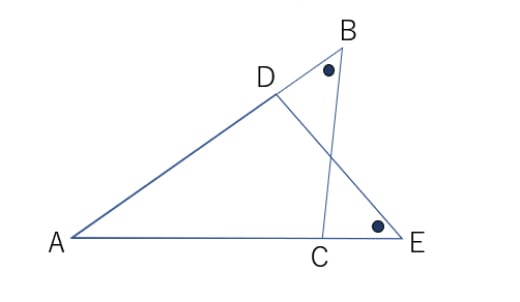



中学数学 証明問題のやり方は 解き方のコツや図形問題への対処法を解説 学びtimes




平行線と線分の比 中学校数学 2018年度高崎経済大学経済学部 地域政策学部入試問題 身勝手な主張
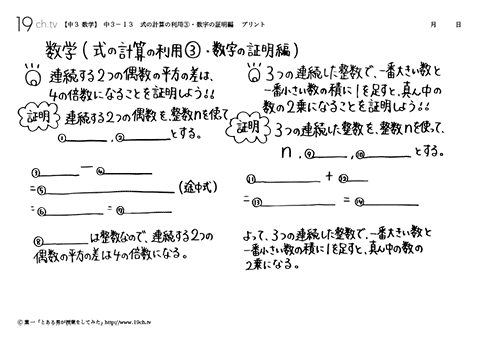



中学3年の数学 動画 式の計算の利用 数字の証明編の問題 19ch




世界一わかりやすい数学問題集中2 4章 平行と合同と証明




三角形の相似条件と証明問題の解き方 数学fun



中3数学12 図形の相似2 相似条件と証明 基本解説プリント 問題 327
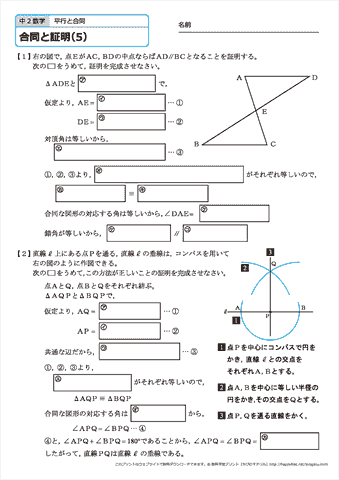



中学2年生 数学 合同と証明 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
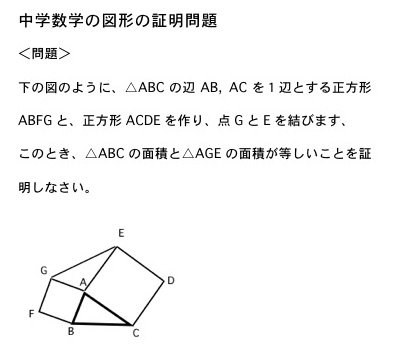



中学生の勉強法と高校受験 בטוויטר 中学数学の図形 三角形と四角形 の証明問題 簡単そうに見えて 少し難しい問題です T Co Kedrtomlsm 中学 数学 中学数学 高校受験 高校入試 中学生 中3 図形問題



子供に中三数学のカレンダー証明問題のやり方を聞かれましたがわ Yahoo 知恵袋
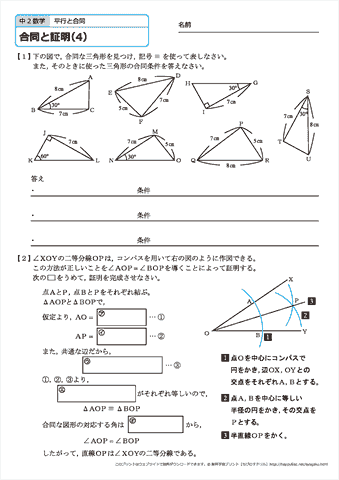



中学2年生 数学 合同と証明 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




数学 中3 14 式の計算の利用 図の証明編 Youtube




中2数学 証明とは 例題編 映像授業のtry It トライイット
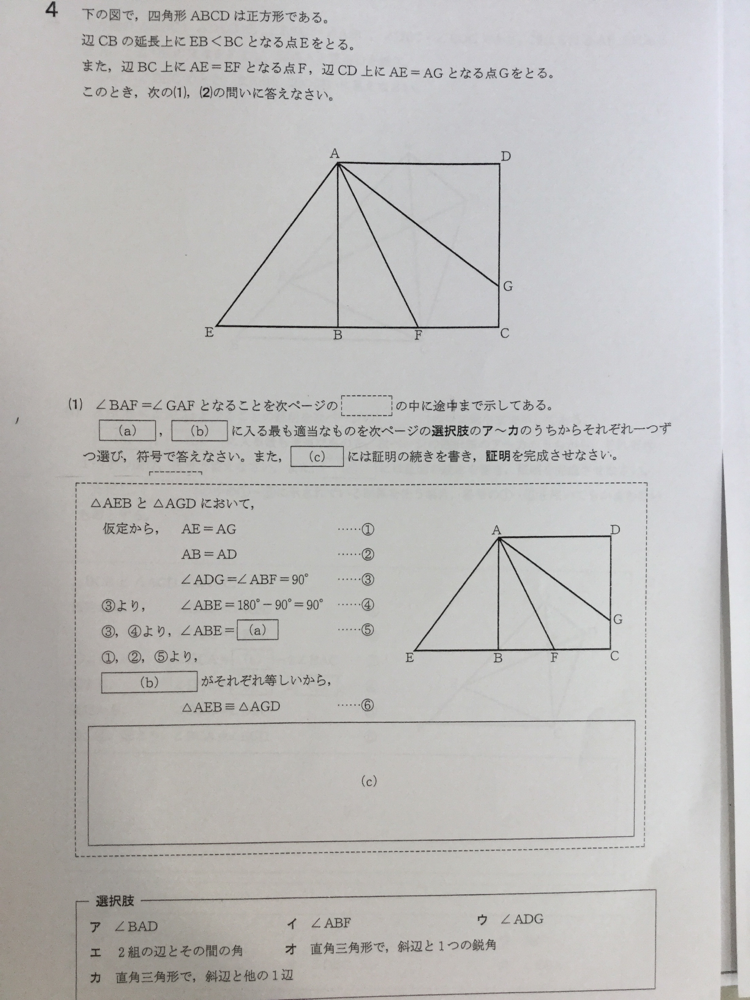



穴埋め式の証明問題の練習してますか かまなび
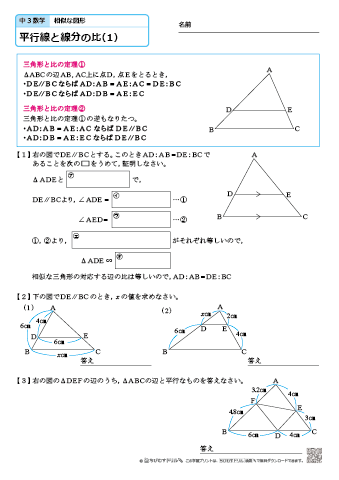



中学3年生 数学 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




中学数学 相似の証明問題の書き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




この様な中学二年生で習う 応用問題である証明問題での質問です この証明問題は Clear
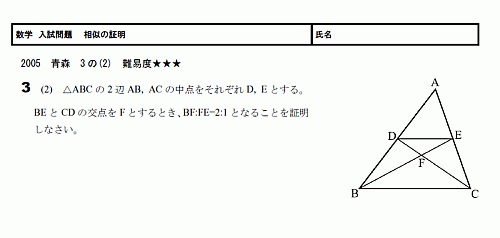



数学 スタディーx




世界一わかりやすい数学問題集中2 4章 平行と合同と証明
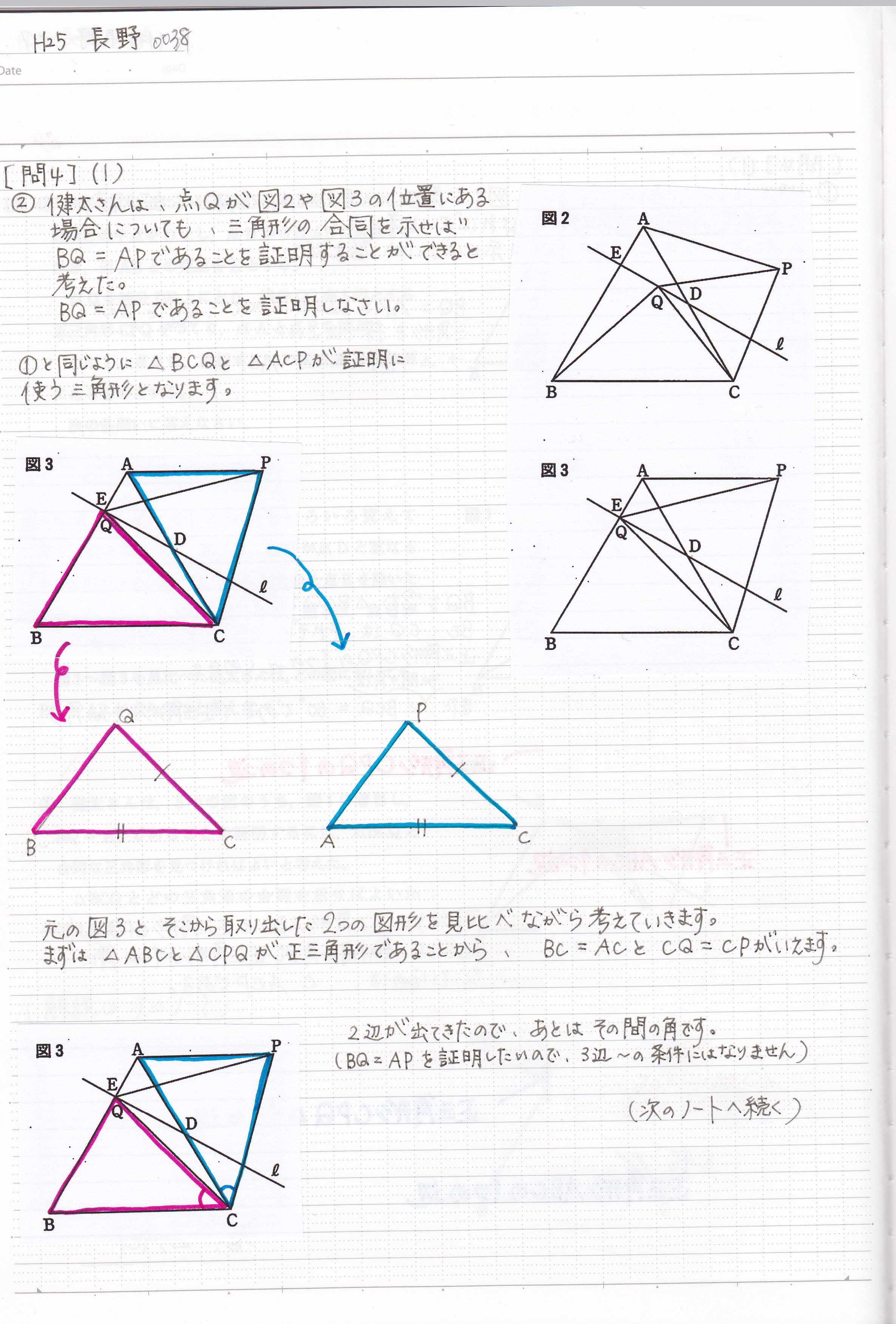



平成25年長野県立高校 入試問題 図形の証明問題 合同 現役塾講師のわかりやすい中学数学の解き方




無料 中3数学 発展 応用問題 問題プリント 334 三平方の定理2




最高中3 数学 相似 子供向けぬりえ
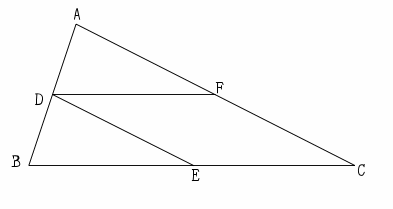



合同の証明2



中学2年生 数学 三角形 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



3




中2数学 基本解説 問題 226 図形6 証明のしくみと根拠 プリント




中3数学 相似の証明問題 練習編 映像授業のtry It トライイット
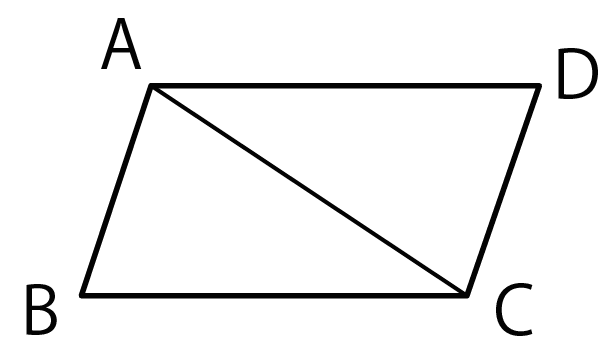



中2数学 図形の証明問題を攻略できる7つのコツ Qikeru 学びを楽しくわかりやすく




相似な図形 補助線を引いて考える相似の問題 中学生からの質問 数学 進研ゼミ中学講座 中ゼミ




中学2年生の数学 証明問題の穴埋めと問題の考え方 塾講師が数学をやりmath
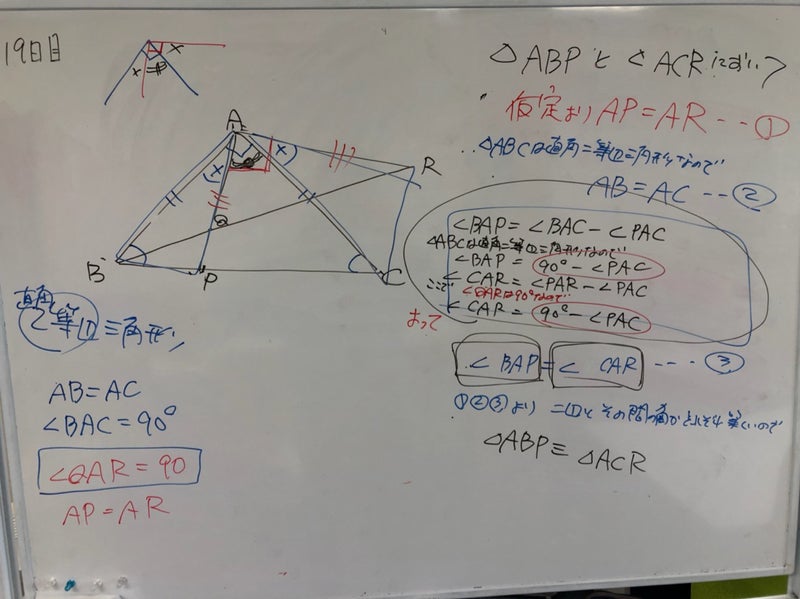



数学の証明問題の解き方 セルモ大蔵 世田谷 の塾長ブログ
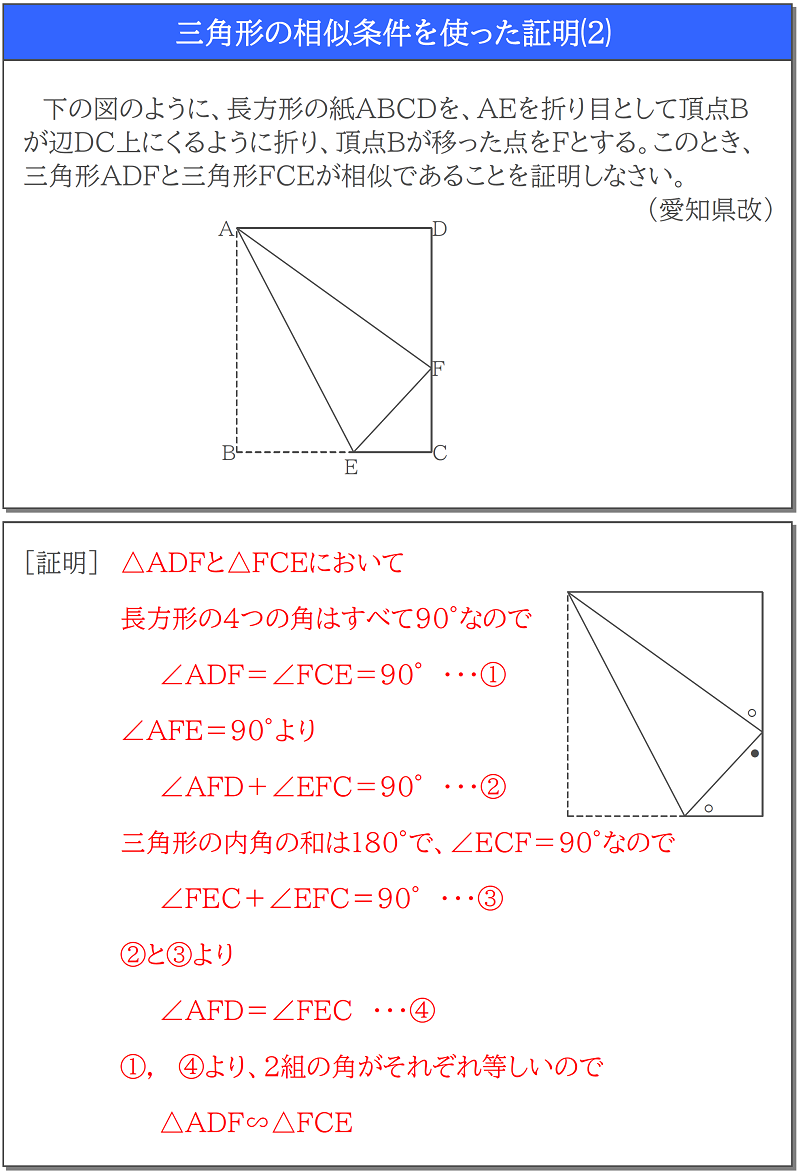



中学3年数学 相似条件を使った証明 2学期期末テスト 赤城 ᐡᐤᐡ




式による証明 無料で使える中学学習プリント
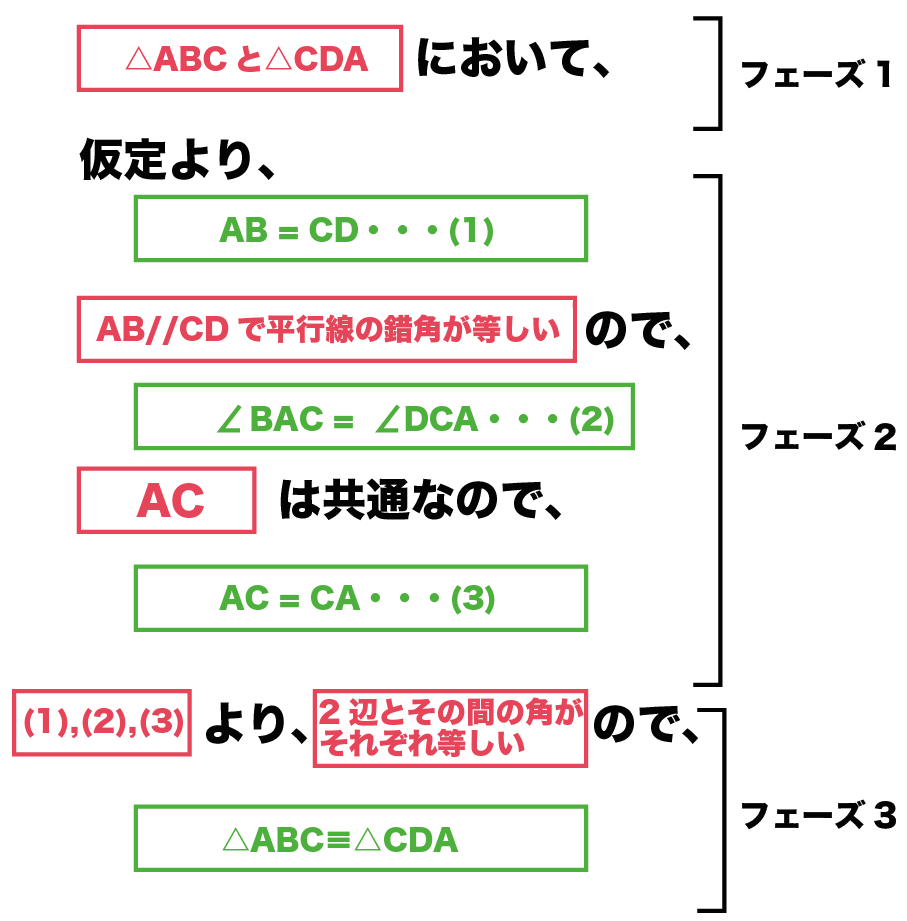



中学数学 3年間つかえる証明問題の書き方 Qikeru 学びを楽しくわかりやすく




中3 数学 オリジナル問題集 解説付き 中学生におすすめです 中学生 Clear
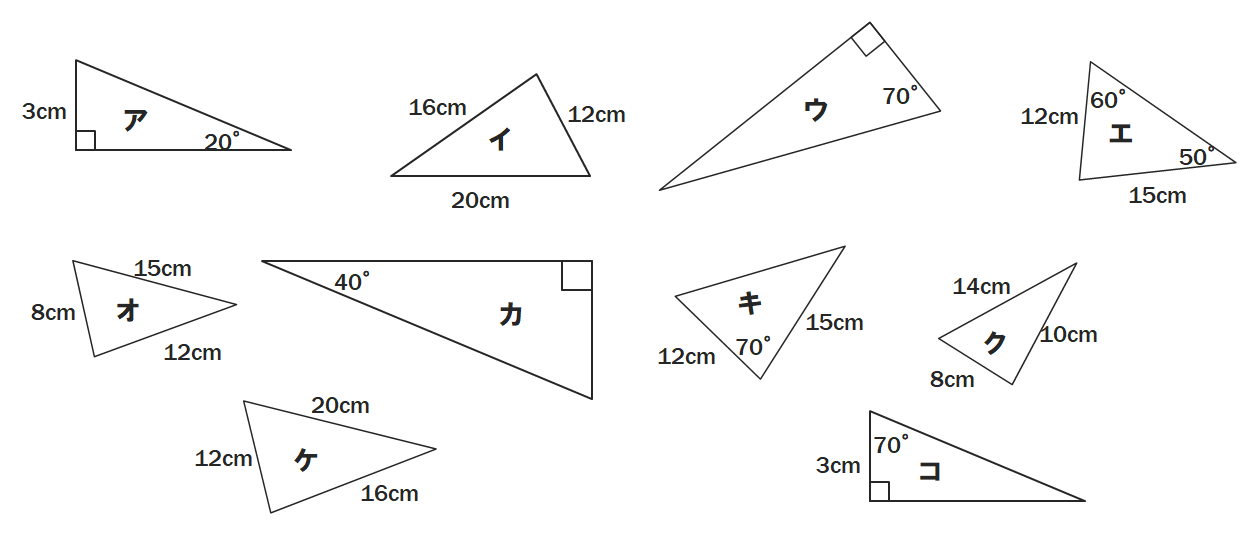



中2数学 3学期学年末テスト予想問題と解答解説 Pikuu




中2 中2 数学 5章 図形の性質と証明 プレイカラー 中学生 数学のノート Clear




図形の折り返しと三角形の相似の証明 解き方 現役塾講師のわかりやすい中学数学の解き方




超 パワーアップ中学数学 図形の証明 中継点 文字式の表現 活用テクニック Myisbn デザインエッグ社 長通 幸大 本 通販 Amazon




苦手な人が多い図形の証明問題を解くコツを解説 実は非常に簡単なんです 学習塾 Step By Step




中2数学 三角形の合同の証明の解き方の手順 こいがくぼ翼学習塾




無料 中3数学 基本問題 解答プリント 図形の相似2 相似条件と証明
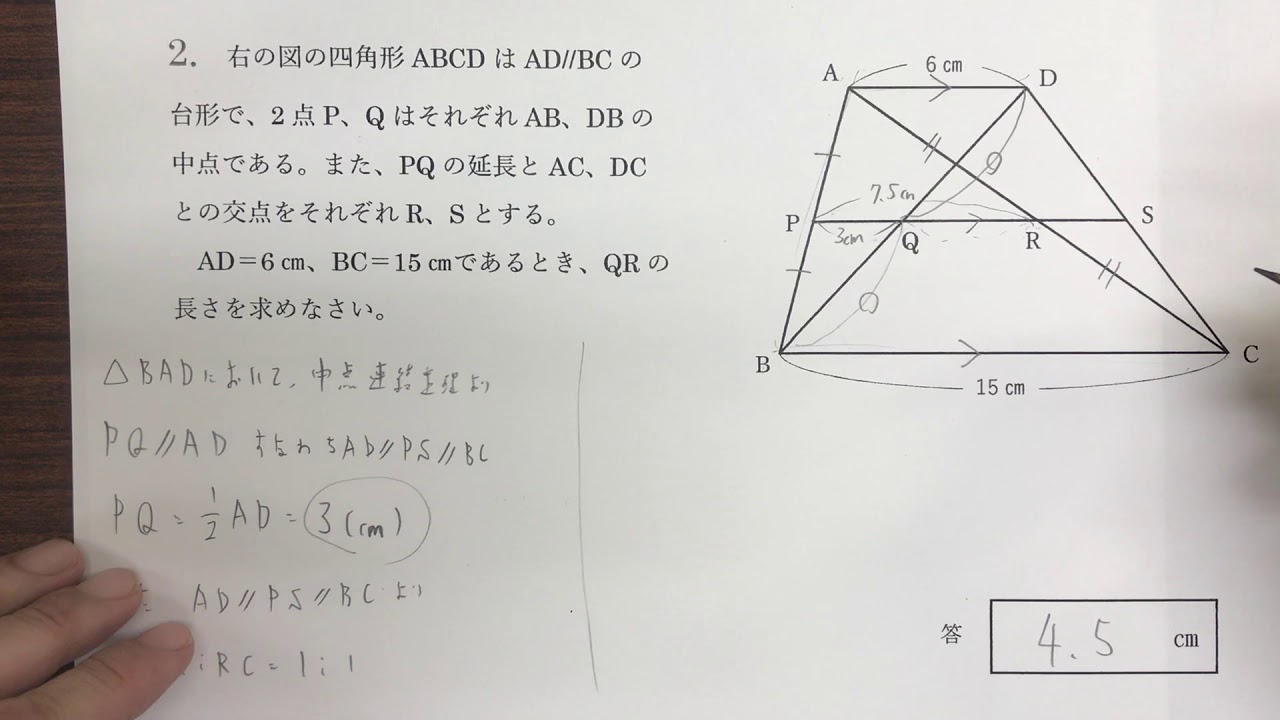



図形 証明 応用問題 相似中心 大問2 中学数学単元別強化教材 これから 図形 紹介動画 3年生2学期レベル Youtube




まる先生 Marusensei8 証明 は3つの証拠をさがそう 1 2 まる練 自宅学習 家庭学習 テスト対策 テスト勉強 マンガで勉強 まる練数学 中学数学 証明問題 三角形の合同 Nitter



中2数学 発展問題プリント12 図形6 証明のしくみと根拠 問題 226
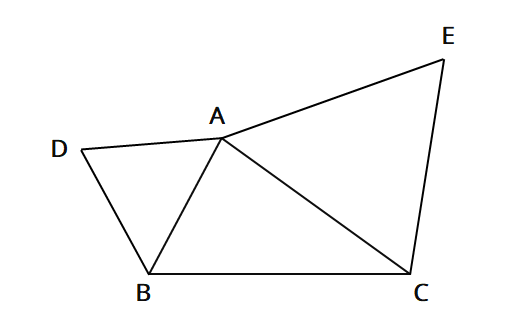



中2数学 三角形の合同の証明応用問題 中学生勉強サイトあかね先生




無料 中2数学 テスト対策 解答プリント 216 図形と合同4 平行四辺形



中2数学 通年用問題集 8章 合同の証明演習




中2数学 証明とは 練習編 映像授業のtry It トライイット



中学数学単元別 平行四辺形 数学 中学校 教材 問題集 5 学林舎 通販 Yahoo ショッピング
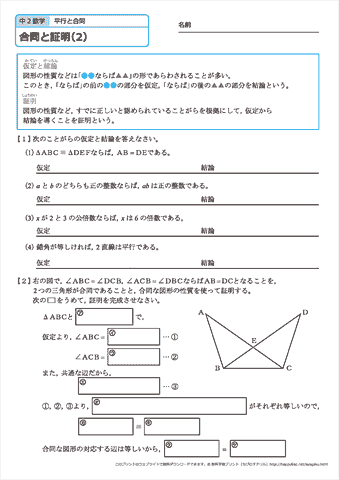



中学2年生 数学 合同と証明 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




平行四辺形の証明問題 無料で使える中学学習プリント




単純閉曲面に囲まれた図形の重心1 中学3年生数学教科書からの三角形の重心についての証明問題 身勝手な主張
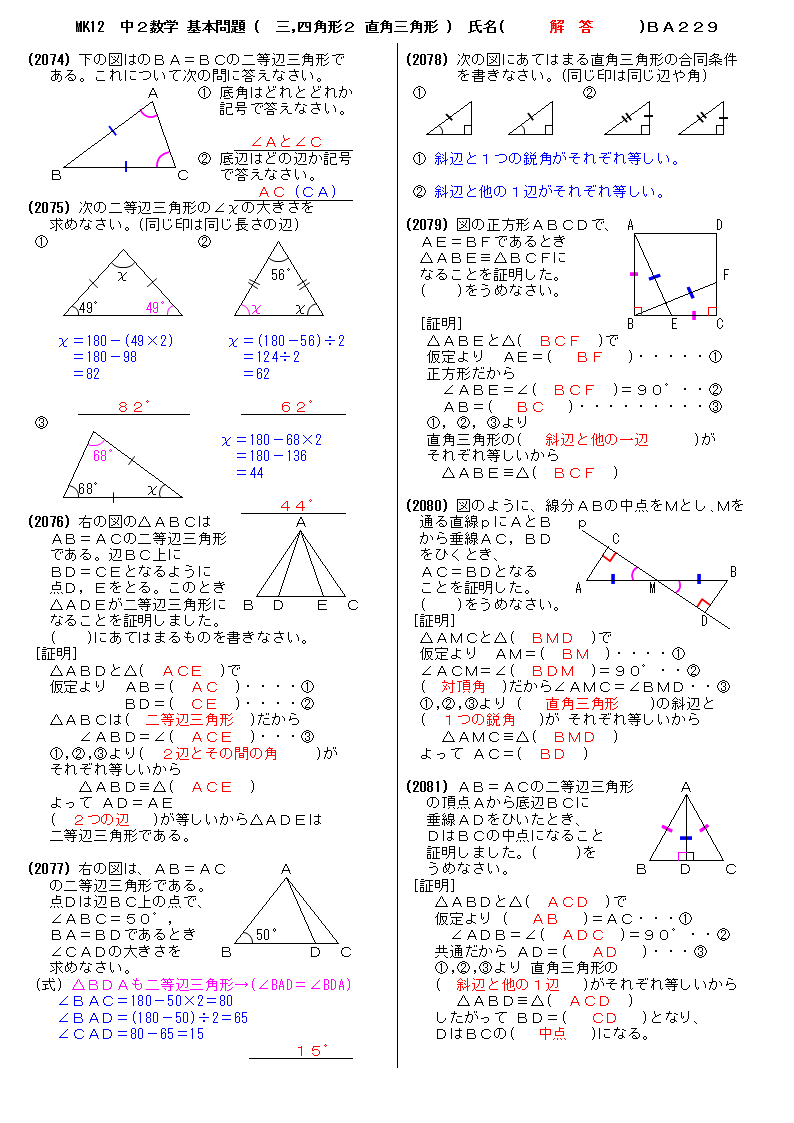



無料 中2数学 基本問題 解答プリント 229 三角形 四角形2 直角三角形
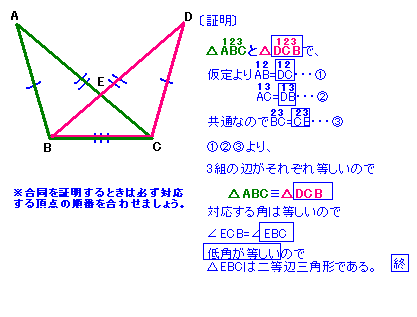



中学数学の問題を解くコツ




中2数学 二等辺三角形の証明 練習編 映像授業のtry It トライイット



1
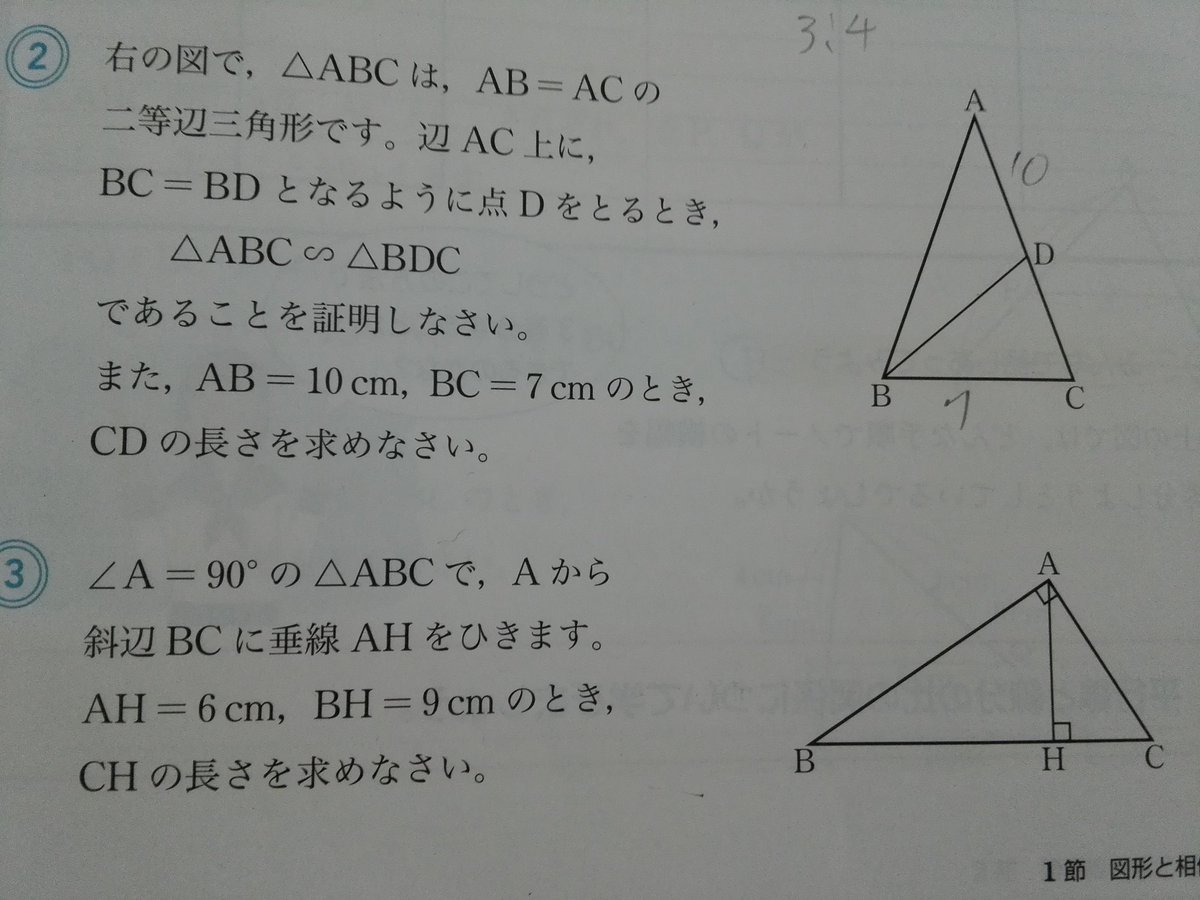



中3数学




数学 中2 60 証明のしくみ Youtube




数学 中3 48 相似の証明チャレンジ Lv 3 Youtube
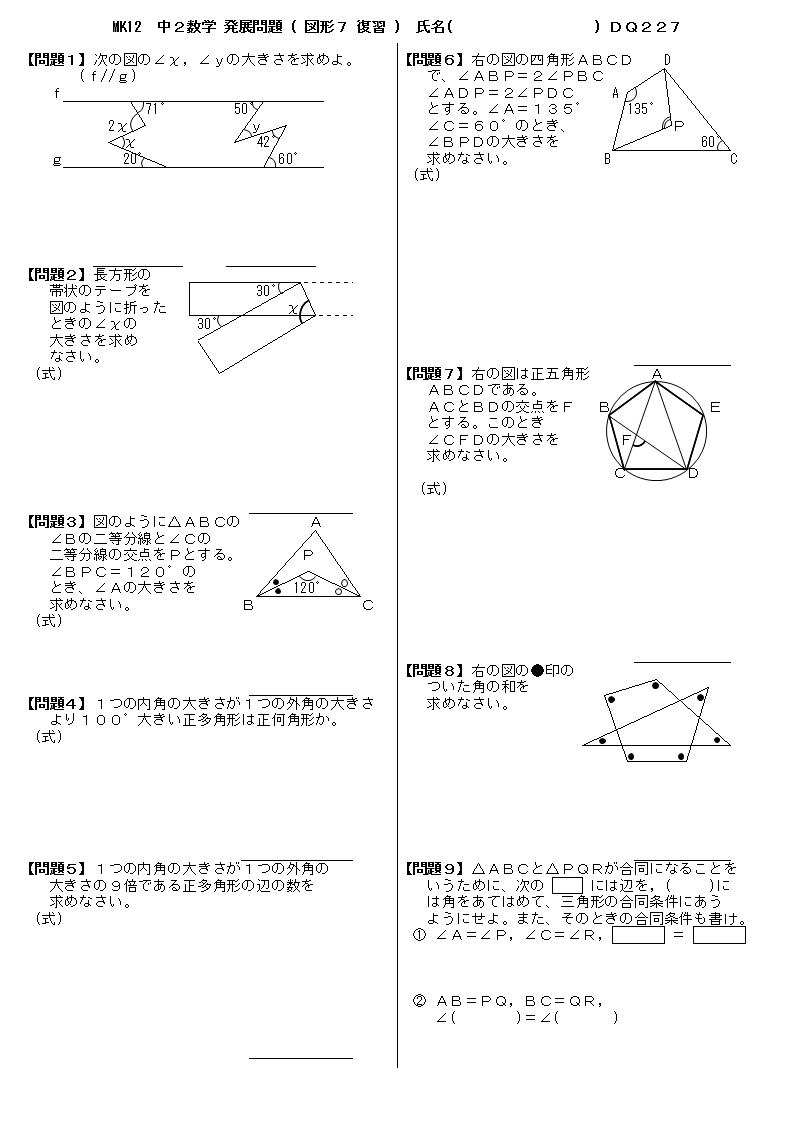



無料 中2数学 応用 発展問題 問題プリント 327 図形の相似2 相似条件と証明




三角形の合同条件と証明問題の解き方 数学fun
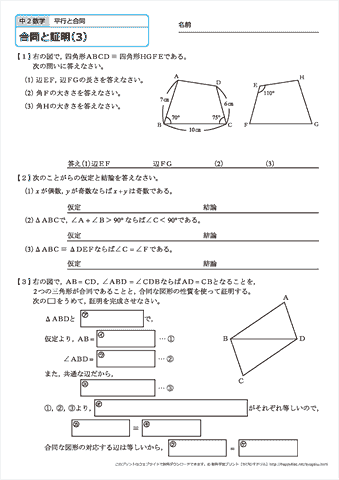



中学2年生 数学 合同と証明 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



0 件のコメント:
コメントを投稿