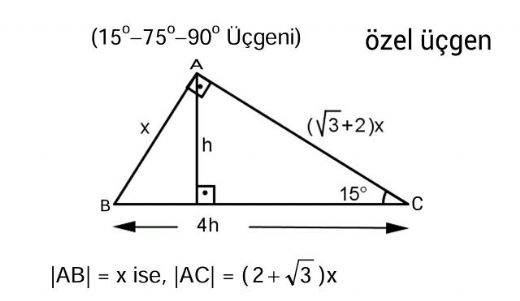
15 75 90 üçgeni özelliklerinin ispatıDaha fazla ispat için http//wwwozelderscicom/matematikformullerininteoremlerininhtmlSitemizi ziyaret e15° – 75° – 90° Dik Üçgeni Yukarıda verilenlere göre, AC kaç cm dir?25/2/13 (30° – 30° – 1°) Üçgeni(30° 30° 1°) üçgeninde 30° lik açıların karşılarındaki kenarlara a dersek 1° lik açının karşısındaki kenar aÖ3 olur 6 (15° – 75° – 90°) Üçgeni (15° – 75° – 90°) üçgenindehipotenüse ait yükseklik AH = h dersek, hipotenüs

Ozel Ucgenler
15 75 90 üçgen alanı
15 75 90 üçgen alanı-Alan = a x b / 2 Şimdi bunu bir örnekle açıklayalım Örnek Dik açının komşu kenarlarından birinin uzunluğu 10 cm iken diğer komşu kenarın uzunluğu 14 cm ise bu dik üçgenin alanını bulalım Verilenleri formülde yerine koyarsak;Ders içeriğini PDF olarak indirmek için http//wwwmetinhocamcom/dikucgen6Tüm PDF'leri tek dosya halinde indirmek için https//drivegooglecom/open?i




Long Term Population Dynamics Of Dreissenid Mussels Dreissena Polymorpha And D Rostriformis A Cross System Analysis Strayer 19 Ecosphere Wiley Online Library
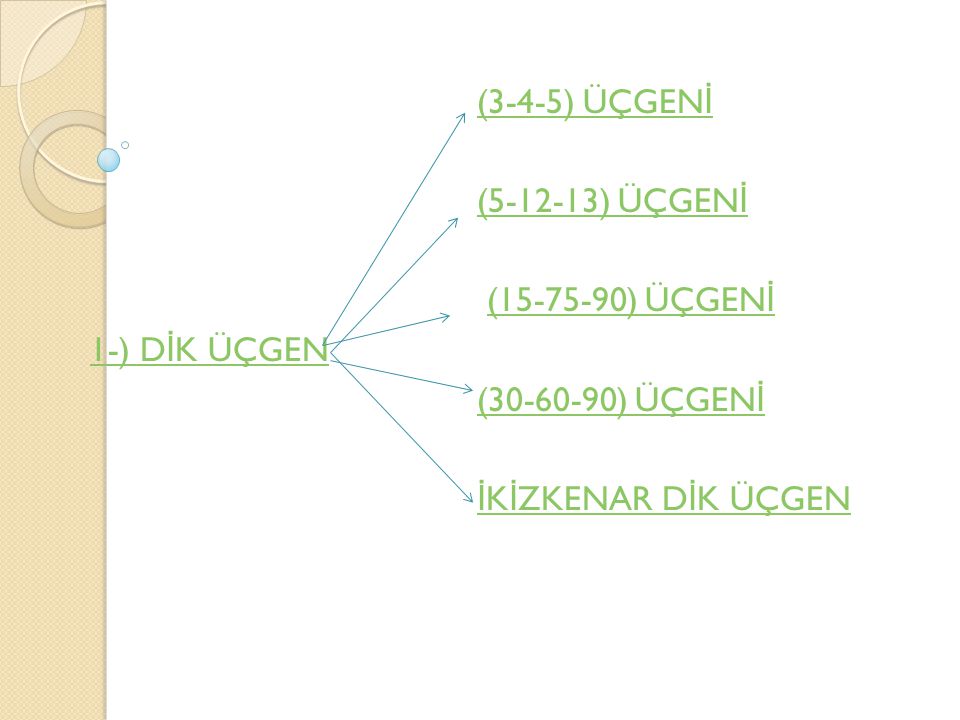
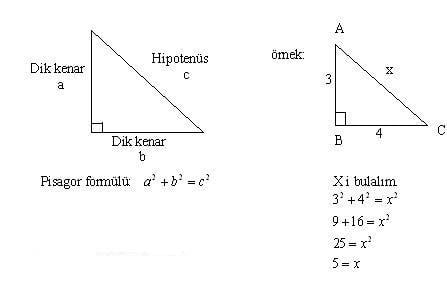
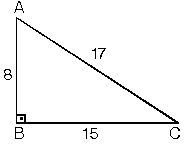
ABC üçgeninde m (A) = 90° a 2 =b 2 c 2 ÖZEL DİK ÜÇGENLER 1 (3 4 5) Üçgeni Kenar uzunlukları (3 4 5) sayıları veya bunların katı olan bütün üçgenler dik üçgendir (6 8 10), (9 12 15), gibi 2 (5 12 13) Üçgeni Kenar uzunlukları (5 12Bulunur ABE üçgeni (15 75 90 ) üçgenidir ABE üçgeninde E nin AB ye en yakın uzaklığı hipotenüse ait yükseklik;13/4/21 Özel üçgenin isminde açıları verilmektedir Burada en önemli şey kenar uzunluklarıdır 45 45 90 Üçgeninde iki açının eşit olması bu açıların baktığı kenar uzunlukları da eşit olması gerekmektedir 90 derece açının karşısındaki kenarın uzunluğu
üçgeni Bu üçgende 15°'lik açının karşısındaki kenar 1 cm ise 75°'lik kenarın karşısındaki kenar 2 3 {\displaystyle 2 {\sqrt {3}}} cm olur İspatı ise 22,567,590 üçgenindeki gibidir Tek farkı, 75°'lik açının 15° ve 60°'lik açılara bölünmesidir Ayrıca bu1/5/21 15 75 90 ÜÇGENİ SORULARI 1 Bir ABC üçgeninde A açısı 90 derece B açısı 75 derecedir Bu üçgende hipotenüse ait yükseklik 3 cm dir Verilen bu bilgilere göre BC kenar uzunluğu kaç cm dir ?12/5/11 Üçgeni Kenar Bağıntısı ( İSPAT ) tenten1 bu konuyu Geometri Formülleri forumunda açtı Cevap 2 Son mesaj 02 Ağu 13, 1933 üçgeni mrdanqerous bu konuyu Özel geometri soruları forumunda açtı Cevap 2 Son mesaj 18 Kas 12, 1806 ABC üçgeni
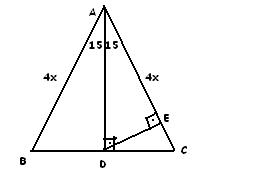
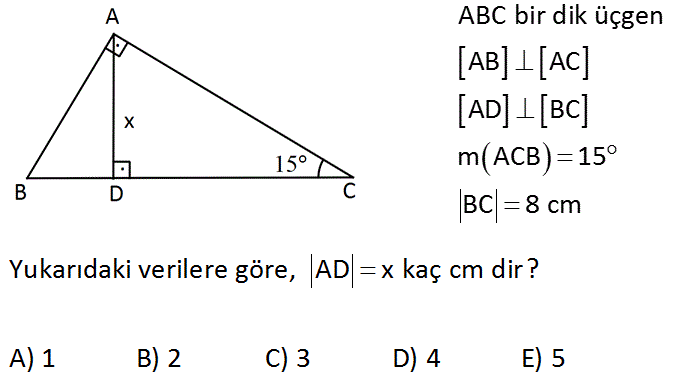
12 A B C E 75 15 H 15 x EH = x uzunluğudur Buradan AB = 4 EH olduğundan, 12 = 4 x x = 3 br bulunur Cevap A'dır (vii)(30 30 1 ) ÜÇGENİ A B C 30 30 1İki taraftan da şimdi 90 çıkaralım x artı x eşittir 90 buluruz Veya 2 x eşittir 90 iki tarafı da 2'ye bölersek, x'i 45 derece olarak buluruz İkizkenar dik üçgenin daha sıklıkla kullanılan ismi, üçgenidir Bir önceki video da üçgeni için yaptığımız gibi, bu videoda bu sefer üçgeninin kenarBu dikmenin uzunluğu hipotenüsün 1/4 katı olur



Out Of Africa Again And Again Nature




15 75 90 Ucgeni Ve Dikdortgende Alan Youtube
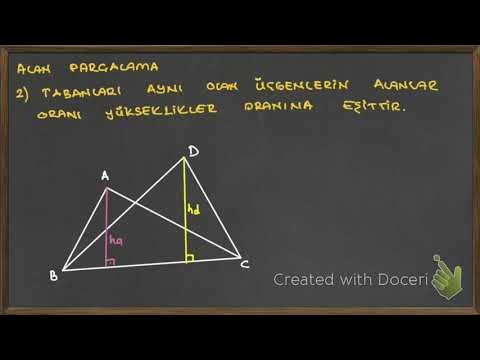
A) 4 B) 6 C) 8 D) 9 E) 12 ÇÖZÜM 2 AED üçgeninin alanı ile DEC üçgeninin alanı aynıdır (Çünkü tabanları ortak ve yükseklikleri eşittir) ECB üçgeni 15 75 90 üçgeni olduğu için, yükseklik 1 hipotenüsün ü dür 4 cm olur 4 A(DEC) 12 cm is e x4 12 4x 24 x 6 cm buluruz(30° – 60° – 90°) Üçgeni ABC eşkenar üçgeni yükseklikle ikiye bölündüğünde ABH ve ACH (30° – 60° – 90°) (15° – 75° – 90°) Üçgeni (15° – 75° – 90°) üçgeninde Eşkenar üçgenin bir kenarına a dersek yük seklik Bu durumda eşkenar üçgenin alanı18/4/21 90 75 15 üçgeni, Bir tür özel üçgendir 90 75 15 üçgeni konusu matematik ve geometri derslerinin bir parçasıdır Öğrencilerimiz okul hayatı boyunca pek çok farklı dersler görüp öğrenmektedir Her sınıfın kendine yaş gurubuna göre belirlenmiş temel matematik ve




Dik Ucgen Konu Anlatimi Ve Ornek Soru Cozumu Kunduz




15 75 90 Ucgeni Webders Net
7 (30° 30° 1°) Üçgeni (30° 30° 1°) üçgeninde 30° lik açıların karşılarındaki kenarlara a dersek 1° lik açının karşısındaki kenar a 3 olur 8 (15° 75° 90°) Üçgeni (15° 75° 90°) üçgeninde hipotenüse ait yükseklik AH = h dersek, hipotenüs BC = 4h olur15 75 90 Üçgeni Kenar Oranları 15 75 90 üçgeni kenarları belirli orana sahiptir Bu oranların ezbere bilinmemesi halinde kendiliğinden bulmak da mümkün olabilmektedir Fakat bu oranları bilmek soruların çözülmesi için daha büyük kolaylık sunacaktır Buna göre 15 75 90 üçgeninde 15 karşısı 1 birim kabul edilirse 75A)8 B)6 C)5 D)4 E)3 30° – 30° – 1° Üçgeni 1° nin karşısındaki kenar, 30° nin karşısındaki kenarın katıdır Yukarıda verilenlere göre, x kaç cm dir?
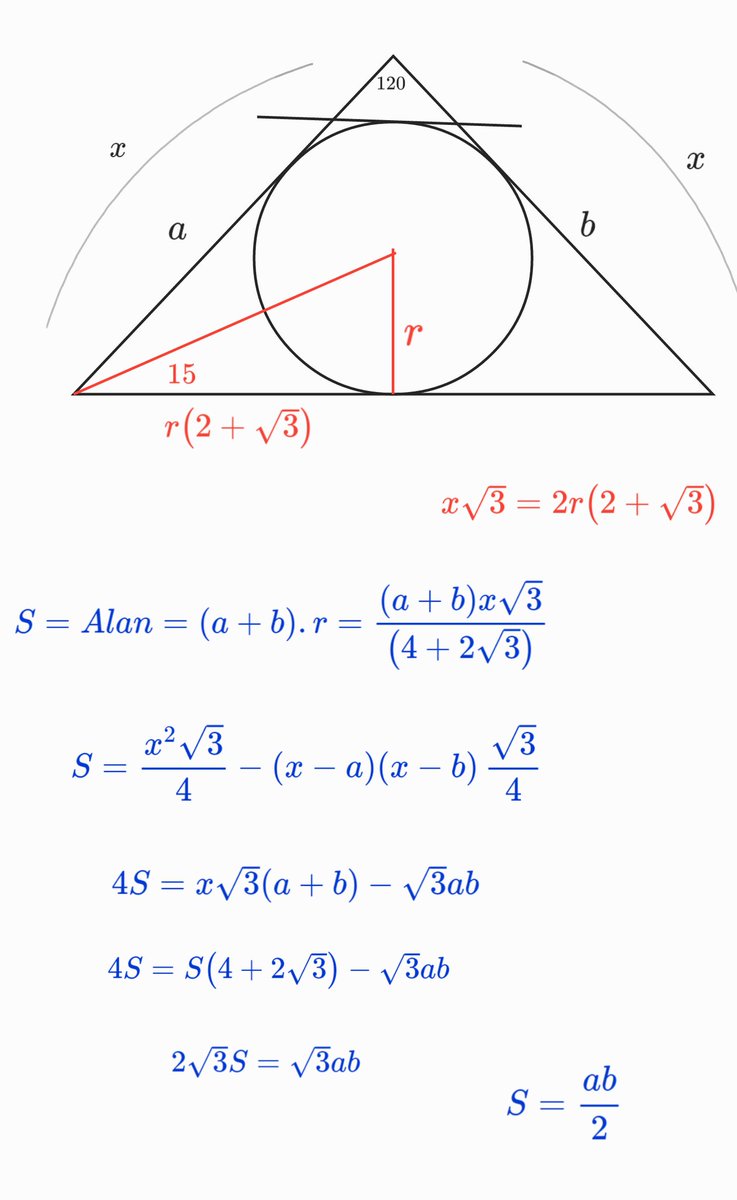



Fatih Saglam Gece Gece Iyi Geldi Kafadagitmaca Bunlarda Ispatlar Cos Teoremi Alanlar Farki Tegetler Dortgeni 15 75 90 Tesekkurler Galois1724 T Co 6fpvza795u T Co Sd9h6pyqqb
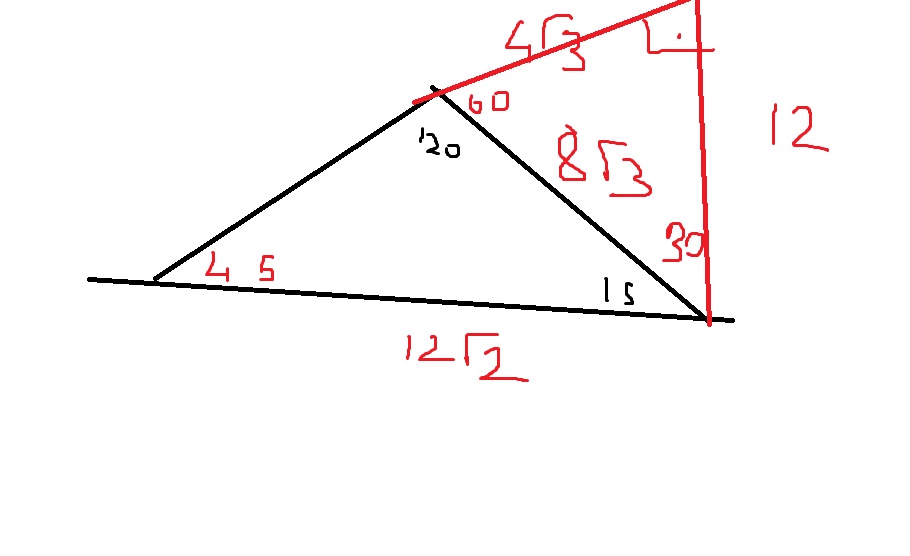



15 75 90 Ucgeni
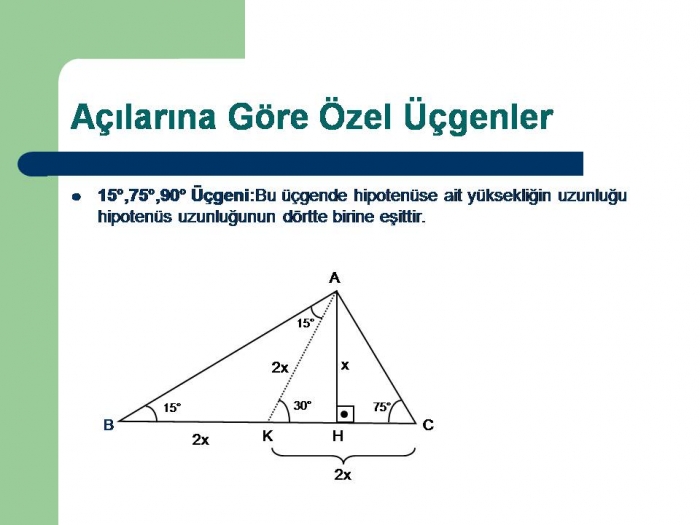
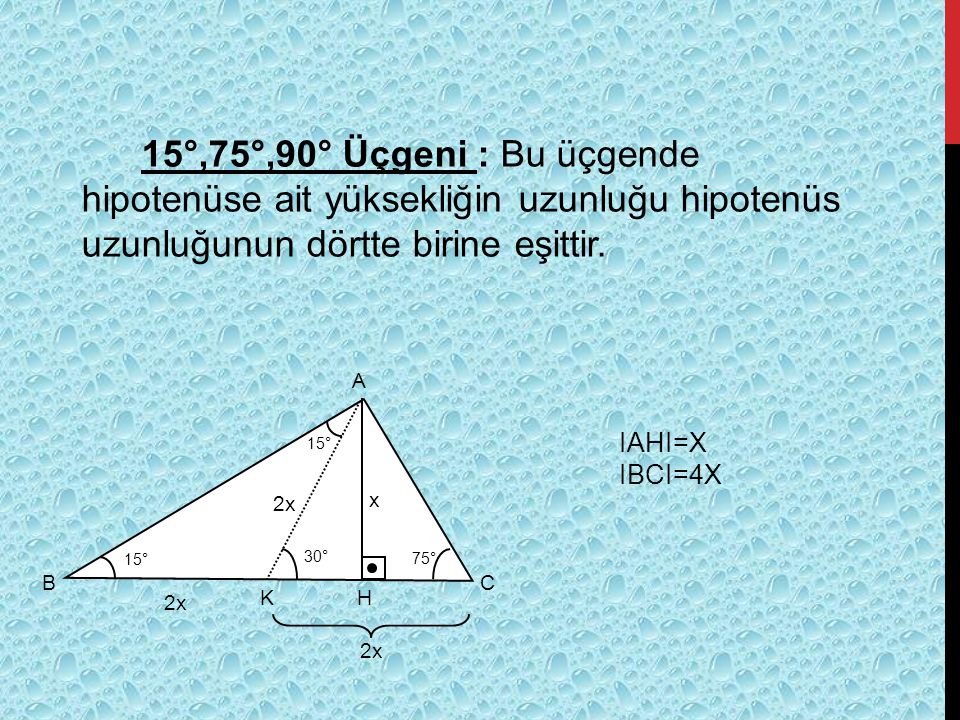
(15° 75° 90°) Üçgeni ile ilgili acil soru Idea question from @aylinaylin123 Geometri25/3/17 16 Özel Üçgenler DİK ÜÇGEN Bir açısının ölçüsü 90° olan üçgene dik üçgen denir Dik üçgende 90° nin karşısındaki kenara hipotenüs, diğer kenarlara dik kenar adı verilir Hipotenüs üçgenin daima en uzun kenarıdırşekilde, m (A) = 90° BC kenarı hipotenüs AB ve AC kenarlarıdik kenarlardır(15° – 75° – 90°) Üçgeni (15° – 75° – 90°) üçgeninde hipotenüse ait yükseklik AH = h dersek, Hipotenüs BC = 4h olur Hipotenüs kendisine ait yüksekliğin dört katıdır İKİZKENAR ÜÇGEN İkizkenar üçgenin tepe açısından tabanına çizilen yükseklik, hem açıortay, hem de kenarortaydır 1




Dik Ucgen 17 22 5 67 5 90 Ucgeni Ders Calisma Ipuclari Evde Egitim Matematik




15 75 90 Ucgeni Ispati Not Bu
Bu özel üçgende 15 derecelik açının karşısında yer alan kenar uzunluğu 1cm alınırsa 75 derecelik açının karşısındaki kenarın uzunluğu 2 √3 cm olur NOT 75 15 90 dik özel üçgeninde eğer hipotenüse bir dik indirilirse;15 75 90 üçgen özelliği ve 15 75 90 üçgeninin 2 pratik kuralı ve örnek çözümlü sorularPratik Geometri Yöntemleri videolarımda sizlere mantık ve pratik yönte1/5/21 15 75 90 ÜÇGENİ ÖZELLİKLERİ 15 75 90 üçgeni bir dik üçgendir İç açıları toplamı 180 derecedir Dış açıları toplamı 360 derecedir İki dar açısının toplamı diğer
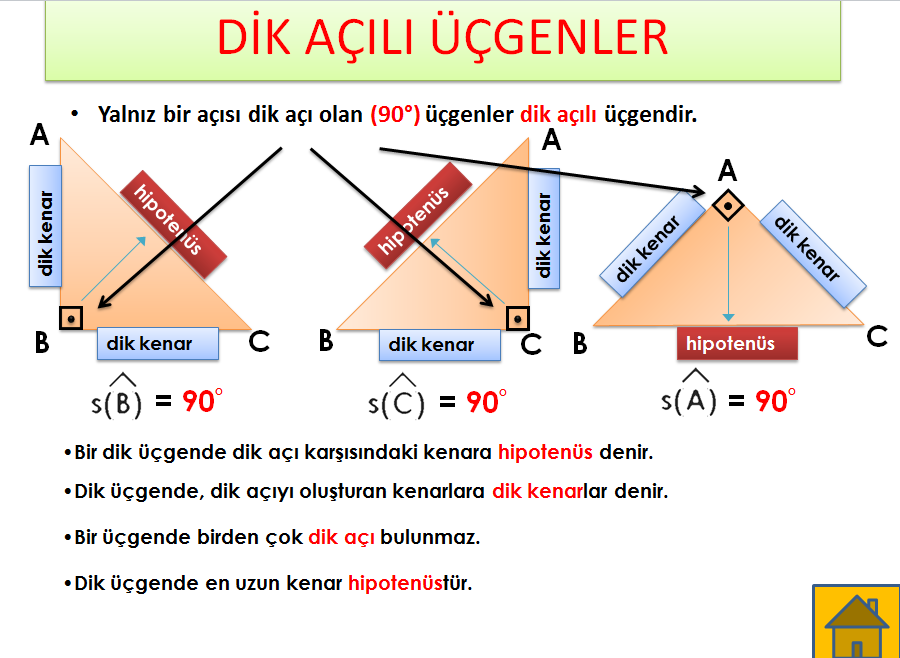



Dik Acili Ucgenin Kenar Ve Aci Ozellikleri Nedir



1
25/2/07 5 (30° 30° 1°) Üçgeni (30° 30° 1°) üçgeninde 30° lik açıların karşılarındaki kenarlara a dersek 1° lik açının karşısındaki kenar aÖ3 olur 6 (15° 75° 90°) Üçgeni (15° 75° 90°) üçgeninde hipotenüse ait yükseklik AH = h dersek, hipotenüs BC = 4h olurKÜME EĞİTİMBUTİK DERSANE ANKARAİLKER ÇORSUZ/3/19 9Sınıf Üçgenin Alanı Konu Anlatımlı Ders Notları – PDF Bu konuda üçgenin alanından bahsedeceğiz Dik açılı üçgen, geniş açılı üçgen gibi üçgen çeşitlerinin alanlarının bulunması, yükseklik ve alan ilişkisi ile üçgenin alan formülünü vereceğiz By



Dik Ucgen Vikipedi




15 75 90 Ucgen Ozelligi Ve 5 Ornek Cozum Youtube
ADE üçgeni ile DEC üçgeni tabanları farklı, yüksek – likleri aynı üçgenlerdir Dolayısıyla alanları oranı 3 A(ADE) 3 olacaktır A(AD 2 10 2 2 E) 15 cm dir ABE üçgeni ile AEC üçgeni15 75 90 ÜÇGENİ VE ÖZELLİKLERİ → 10Sınıf Matematik Dik Üçgen sunusunun 30 30 1 ÜÇGENİ VE ÖZELLİKLERİ slaytını görüntülemektesinizAD C üçgeni 15 75 90 üçgenidir 15 75 90 üçgeninde hipotenüse inen yükseklik, hipotenüsün 4' te 1'i dir 4 2 x 2 cm bulunur 4 12 ABC eşkenar üçgen, AB // AD AE AD ED 2 cm Yukarıdaki verilere göre, BE x kaç cm dir?




Ozel Ucgenler




Dik Ucgen Konu Anlatimi Ve Ornek Soru Cozumu Kunduz
22/3/04 75 dereceyi 1560 derece olacak şekilde ayıran bir kenar çizip karşı dik kenar ile birleştirirsek, bir tarafta ikizkenar üçgen diğer tarafta üçgeni oluşur ve kenar uzunlukları arasındaki bağıntı ezberlenmemiş olur dik kenarlar arasındaki bağıntıyı hatırlayacak olursak, 15 in karşısındaki kenar "a" ise 75 in karşısındaki kenar "2aakök3" aynı yolla 2227/3/21 15 75 90 üçgeni, üçgenler geometrinin temelini oluşturmaktadır Düzlemde doğrusal olmayan 3 noktanın birleşmesi ile oluşan geometrik şekildir Üç kenarı ve üç köşesi bulunan üçgenlerin 4 çeşidi bulunmaktadır Çeşitkenar üçgen, ikizkenar üçgen ve eşkenar üçgendir15 75 90 üçgeni 30 60 90 üçgeni 37 53 90 üçgeni 45 45 90 üçgeni 1 1 atalante #7593 2108 ~ 370 22,5 67,5 90 üçgeni oldum olası kim bulmuş diye merak ettiğim üçgendir lakin çözümü oldukça basittir 67,5 olan açıyı 22,545 olarak ayırırsınız,




Dik Ucgenler Pisagor Teoremi Konu Anlatimi Soru Cozumleri Ders Notu 9 Sinif Matematik Tyt
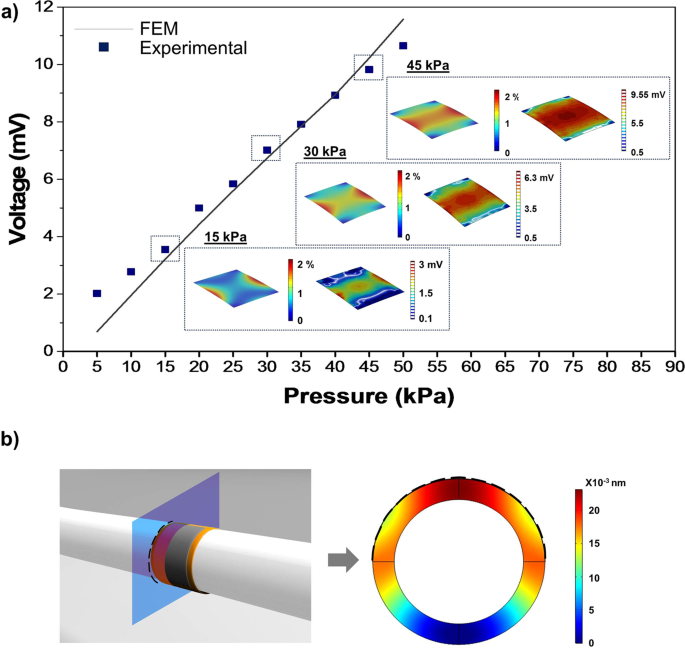



Soft And Flexible Piezoelectric Smart Patch For Vascular Graft Monitoring Based On Aluminum Nitride Thin Film Scientific Reports
14/9/ Üçgende Açılar konusu, TYT ve AYT Matematik testlerindeki Geometri kısmı için temel konulardan biri olduğundan iyice pekiştirmen önemli 30 60 90 Üçgeni, 45 45 90 Üçgeni, 30 30 1 Üçgeni, 15 75 90 Üçgeni, Üçgende İç Açılar Toplamı, Dış Açılar Toplamı, Roket Kuralı gibi alt başlıklar pek çok bilgi ve kavram içeriyor8/2/21 15 75 90 özel üçgeninin altın kuralı 15 derecenin karşısı 1 birim ise 75 derecenin karşısı √3 2 birim olmak zorundadır Hipotenüs ise 8 4√3 olarak hesaplanır Yukarıdaki kuralı uygulayabilmeniz için 15 75 90 özel üçgeninin var olması gerekiyor Bu üçgeni soru çözümlerinde sizler de elde edebilirsiniz14/5/13 (15° – 75° – 90°) Üçgeni (15° – 75° – 90°) üçgenindehipotenüse ait yükseklik AH = h dersek, hipotenüs BC = 4h olur Hipotenüs kendisine ait yüksekliğin dört



Arc High Resolution Stock Photography And Images Alamy
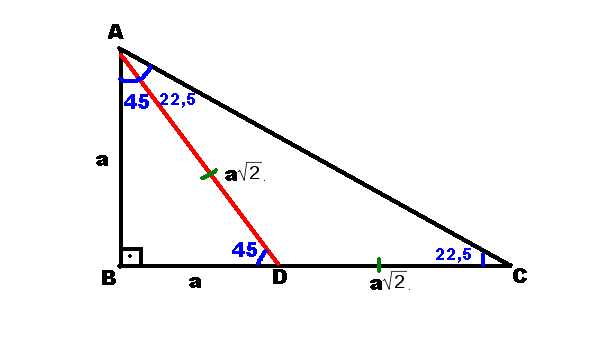



22 5 67 5 90 Ucgeni 1 2 Ispat
Proof Without Words kitabından şahane bir sözsüz kanıtDaha fazlası MY VİDEO EĞİTİM SİTESİ'nde Misafir olarak giriş yapabilirsiniz Detaylar için wwwmustaf1/1/08 özel bir dik üçgendir 90 derecelik açının karşısında hipotenüs bunulunur Bu 90 derecelik açının olduğu yerden hipotenüse indirilecek dik Kenar uzunlukları veya katları şeklinde olan dik üçgenlerdir Üçgeni Kenar uzunlukları veya katları şeklinde olan dik üçgenlerdir AÇILARINA GÖRE ÖZEL DİK ÜÇGENLER Üçgeni Üçgeni 0 Üçgeni Üçgeni İKİZKENAR ÜÇGEN İkizkenar üçgende tepe açısından inen;
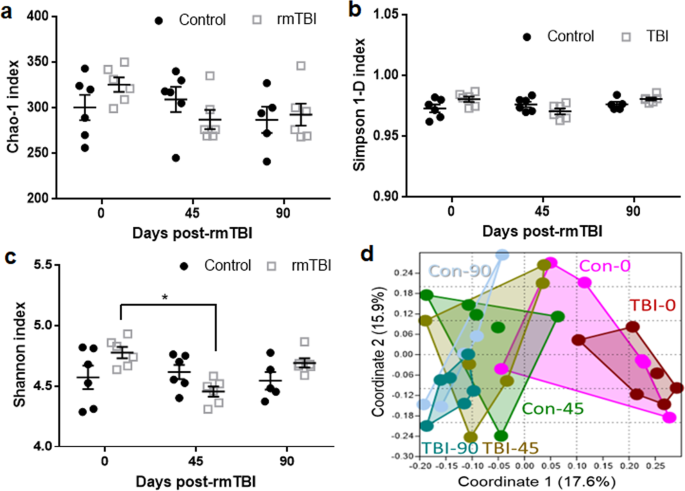



Repetitive Mild Traumatic Brain Injury Results In A Progressive White Matter Pathology Cognitive Deterioration And A Transient Gut Microbiota Dysbiosis Scientific Reports




15 75 90 Ucgeni Ozellikleri Ve Kurali Ogrenci Yardim
12/2/ Bir dik üçgenin alanı, dik kenarların çarpımının yarısına eşittir Bir dik üçgenin iç teğet çemberinin hipotenüs üzerinde ayırdığı parça uzunlukları m ve n ise alanı mn ile bulunur Özel dik üçgenlerden olan 15 – 75 – 90 üçgeninde dik açıdan indirilen yükseklik, hipotenüs uzunluğunun ¼DİK ÜÇGENİN ALANI Diküçgenin alanı, dik 15 75 90 üçgeni ile ilgili bilmemiz gereken ve çok basit olan bir dikme özelliği vardır 15 75 90 üçgeni içerisinde 90 dereceden hipotenüse indirilen bir dikmenin uzunluğu hipotenüsün 4'te biri kadar olur Yani dikme ile hipotenüs arasında h 4h bağıntısı vardır




Murat Sen Akdeniz Universitesi Ucgenler Ppt Video Online Indir
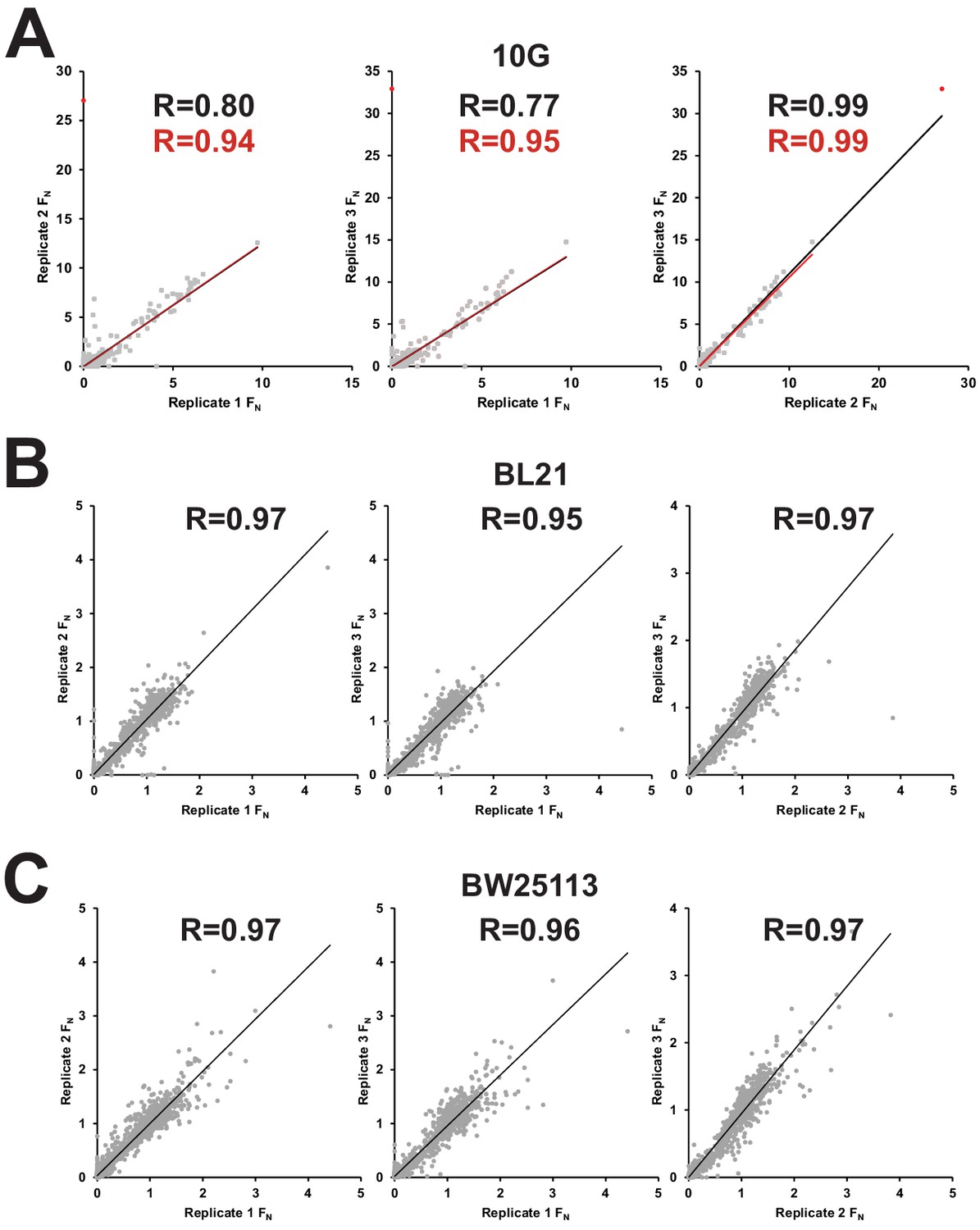



Mapping The Functional Landscape Of The Receptor Binding Domain Of T7 Bacteriophage By Deep Mutational Scanning Elife
7/4/21 15 75 90 üçgeni özellikleri Bir dik üçgendir İki dar açısının toplamı dik açısını vermektedir İki dar açı karşısındaki dar kenarlarının toplamı her daim dik açının karşısındaki geniş kenar uzunluğunu vermek zorundadır İki dar açının oranı 1/5 olmak zorundadır19/4/21 Bunlar 15° 75° 90° üçgeni, 30° 60° 90° üçgeni ve 15° 15° 150° üçgenidir Bu üçgende 15°'lik açının karşısındaki kenar 1 birim ise 75°'lik kenarın karşısındaki kenar 2 √3 birim olur İspatı ise 22,5° 67,5° 90° üçgeninde olduğu gibidir(15 75 90) Üçgeni (15 75 90) Üçgeni konusunu önce anlatıyoruz hemen ardından etkileşime geçmesini sağlıyoruz Bu şekilde kalıcılığı ve öğrenmeyi sağlıyoruz




Ucgenin Alani Nasil Bulunur Ucgen Alan Formulleri Ve Cesitleri Bilgeniz Com



2 Kok 5 3 Ucgeni
Dik üçgenin alanı öğrenilirken aşağıdaki formül kullanılmaktadır Bu formül;17 Ocak 12 16 Ocak 12 xMaTeMaTiK 0 yorum (15° 75° 90°) Üçgeni, (3 4 5) Üçgeni, (30° 30° 1°) Üçgeni, (30° – 60° – 90°) Üçgeni, (5 12 13) Üçgeni, İkizkenar dik üçgen, İKİZKENAR ÜÇGENI, ÖKLİT BAĞINTILAR, Üçgenlerde UzunlukBir üçgende iç açıları toplamı 180 derece olduğu için diğer açı 1 = 15 işleminden 15 derece olarak bulunur Yani bu üçgen 15 75 90 üçgenidir




Overcoming The Challenges Associated With Image Based Mapping Of Small Bodies In Preparation For The Osiris Rex Mission To Bennu Dellagiustina 18 Earth And Space Science Wiley Online Library
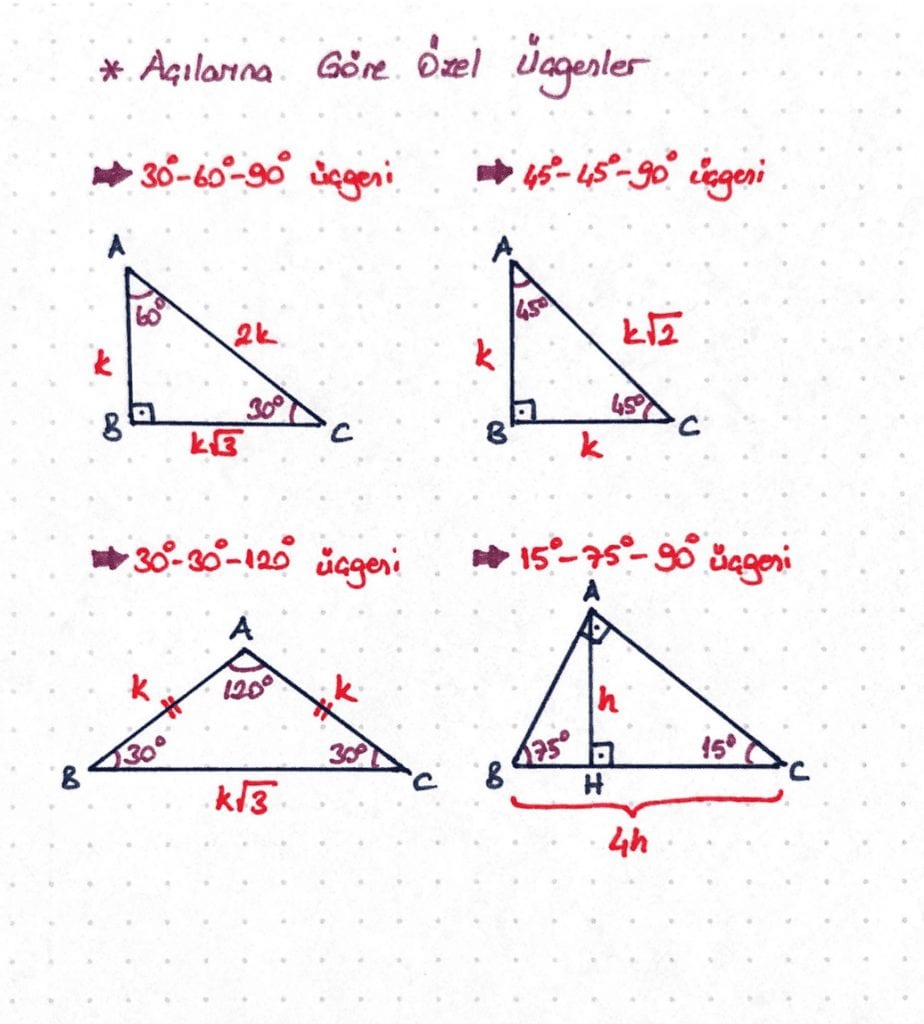



15 75 90 Ucgeni Ucgende Acilar Ders Notlari Kunduz
üçgeni 22,5 derecenin karşısındaki kenar " a " ise 67,5'un karşısındaki kenar " aakök2 " dir bir de hipotenüs ile ona ait yükseklik arasında bi bağıntı vardır hipotenüse ait yükseklik " h " ise hipotenüs " 2kök2h " dır düzgün sekizgende çok karşımıza çıkar düzgün bir sekizgenin en uzun veya1/8/13 Üçgeni Kenar Bağıntısı ( İSPAT ) ABC Üçgeninin Alanı = 1/24x4xsin30 olmak üzere 4x²dir ADC Üçgeninin alanı da bunun yarısı 2x²'dir Aynı zamanda ADC üçgeninin Alanı = 1/24xDE 'dir 2x² = 2xDE DE=x bulunur ve üçgeninde AC uzunlugu DE uzunlugunun her zaman 4 Katıdır 02 Ağu 13 1858 #231/1/21 15 75 90 üçgeni özellikleri çoğu zaman dik bir üçgene dikme indirildiğinde ortaya çıkar Görselden de gördüğünüz gibi dik üçgenin, dik açısından tabana doğru bir dikme indirilmiş Daha sonra karşımıza iki adet 15 75 90 üçgeni çıkmış



15 75 90 Ucgeni Ucgende Acilar Ders Notlari Kunduz



3
a) 60 b) 75 c) 90 d) 135 e) 150 (01 Öss) 17 Komşu ve bütünler iki açının açıortayları arasındaki açının ölçüsü 90° olduğundan m(DAE) = 90° ve DAE üçgeni ikizkenar dik üçgen olduğundan m(ADC) = 45° dir m(ABC) = x ve m(ACE) = y dersek ABC üçgeninde açıortaylar arasındaki açı özelliğinden225 (30° 30° 1°) Üçgeni (30° 30° 1°) üçgeninde 30° lik açıların karşılarındaki kenarlara a dersek 1° lik açının karşısındaki kenar aÖ3 olur 6 (15° 75° 90°) Üçgeni (15° 75° 90°) üçgeninde hipotenüse ait yükseklik AH = h dersek, hipotenüs BC = 4h olur




Ozel Ucgenler Ders Notu Konu Anlatimi Ders Notu




15 75 90 Ucgeni Ucgende Acilar Ders Notlari Kunduz




Chapter 5 2b Erebus Volcanic Province Petrology Geological Society London Memoirs
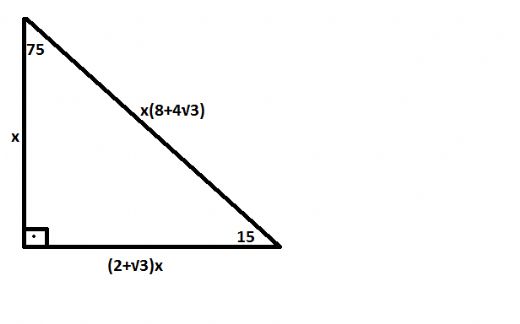



15 75 90 Ucgeninin Ozellikleri Nelerdir Ucgen Gen Tr




Eskenar Ucgen Alani Not Bu




15 75 90 Ucgeni
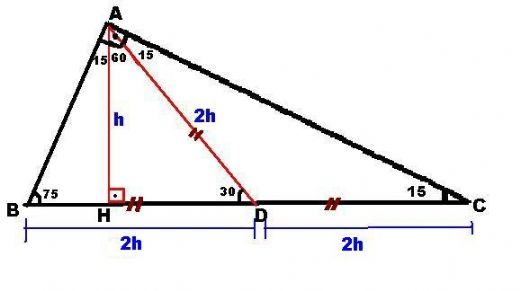



15 75 90 Ucgeni Ozellikleri Acilar Gen Tr




15 75 90 Ucgeni Akilli Geometri



3
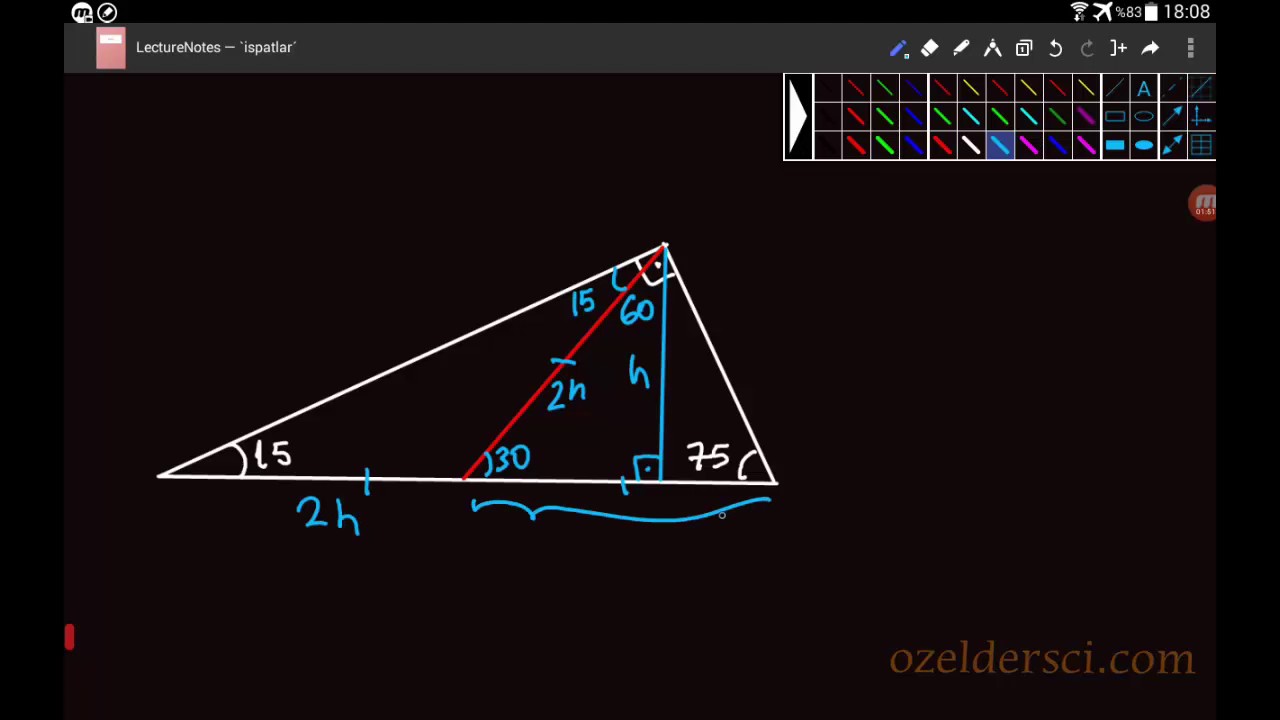



15 75 90 Ucgeni Ozelliklerinin Ispati Youtube




Economists And Public Opinion Expert Consensus And Economic Policy Judgments The Journal Of Politics Vol 78 No 2
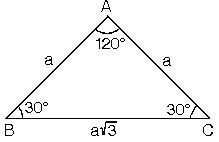



Dik Acili Ucgenin Kenar Ve Aci Ozellikleri Nedir




Directional Semivariogram Analysis To Identify And Rank Controls On The Spatial Variability Of Fracture Networks Sciencedirect




15 75 90 Ucgeni Ozellikleri Ve Kurali Soru List
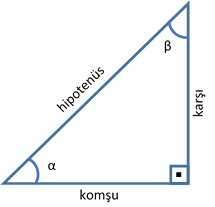



Dik Ucgende Trigonometrik Hesaplamalar




15 75 90 Ucgen Ozelligi Ve 5 Ornek Cozum Youtube
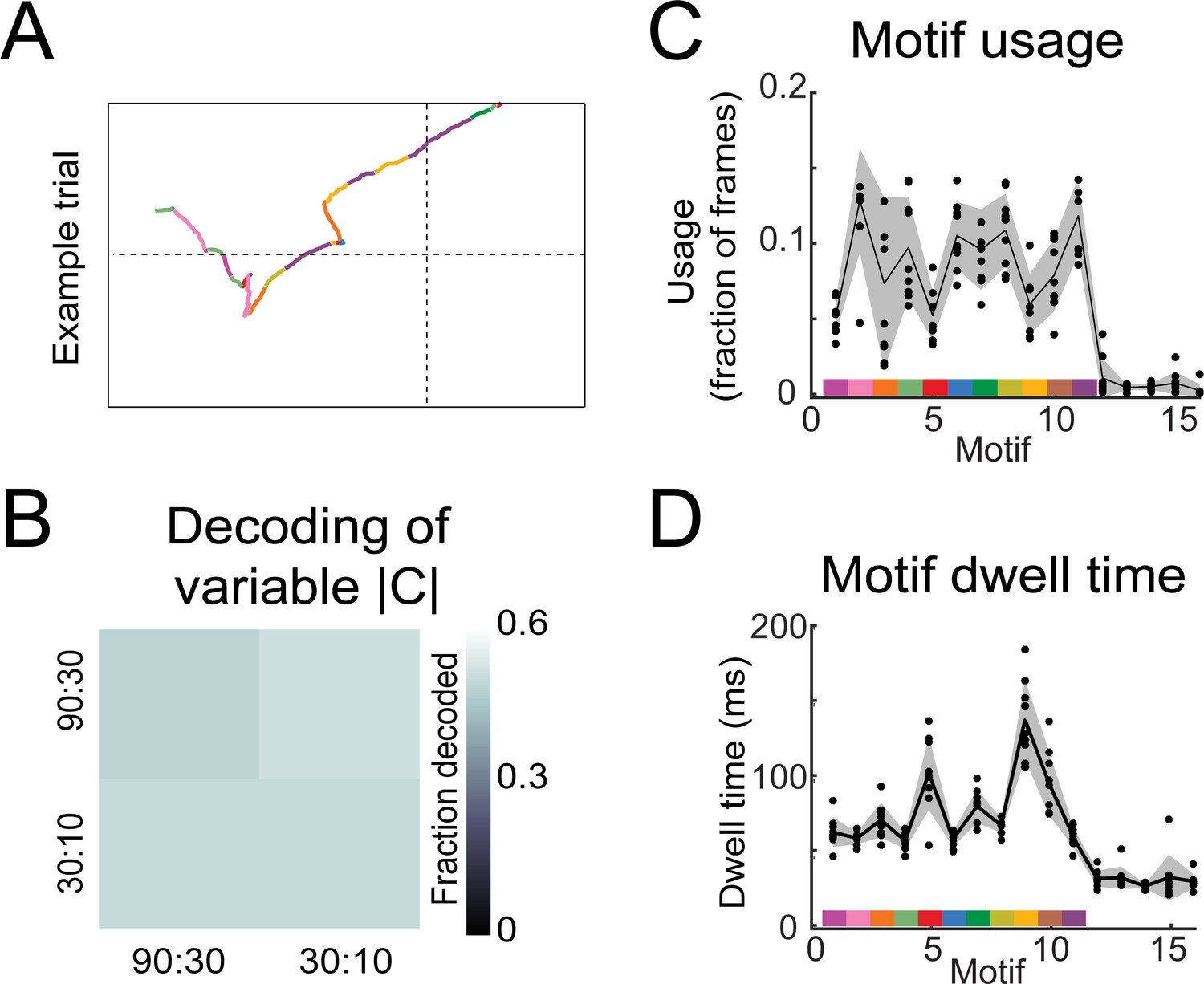



Sniff Synchronized Gradient Guided Olfactory Search By Freely Moving Mice Elife
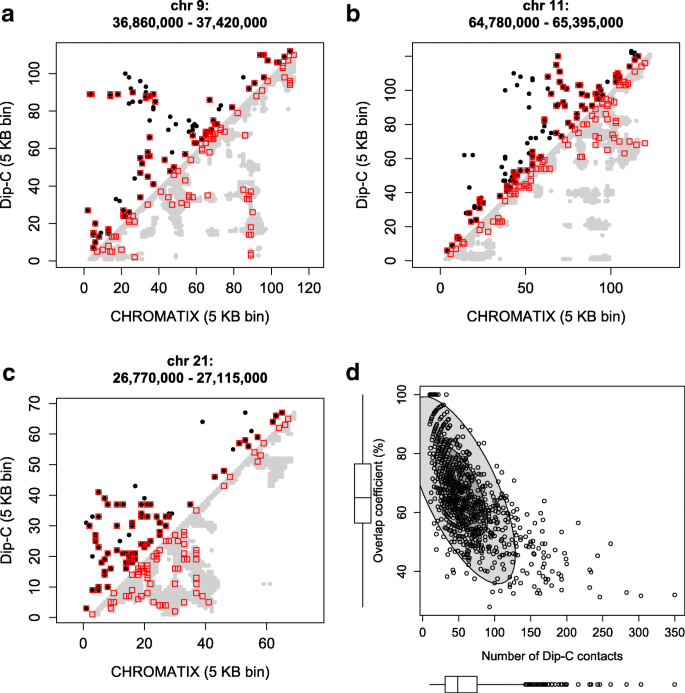



Chromatix Computing The Functional Landscape Of Many Body Chromatin Interactions In Transcriptionally Active Loci From Deconvolved Single Cells Genome Biology Full Text
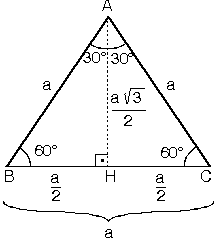



Dik Acili Ucgenin Kenar Ve Aci Ozellikleri Nedir



15 75 90 Ucgeni Uludag Sozluk




Ozel Ucgenler Nelerdir Ozel Ucgenler 8 15 17 7 24 25 30 60 90 Ve Diger



Ozel Ucgenler Ozel Ucgenler Icindekiler Pisagor Bagintisi Oklit Bagintilari Kenarlarina Gore Ucgenler Acilarina Gore Ucgenler Kazanimlar Kaynakca Ppt Video Online Indir



Genomic Risk Score Offers Predictive Performance Comparable To Clinical Risk Factors For Ischaemic Stroke Nature Communications




The Osmolyte Tmao Modulates Protein Folding Cooperativity By Altering Global Protein Stability Biochemistry



Polymers Free Full Text Electrical And Electrochemical Properties Of Conducting Polymers Html



15 75 90 Ucgeni Kenar Bagintisi Ispat




Dik Ucgen 6 15 75 90 Ucgeni Geometri Metin Hocam Youtube



Dik Acili Ucgenin Kenar Ve Aci Ozellikleri Nedir



Ucgenlerde Alan Oranlari




Bir Sozsuz Kanit 15 75 90 Ucgeni Youtube




Dik Ucgen 15 75 90 Ucgeni Islemli Em Iyi Secicem Gereksiz Engellenir Eodev Com



Galactic And Extragalactic All Sky Murchison Widefield Array Gleam Survey Ii Galactic Plane 345 L 67 180 L 240 Publications Of The Astronomical Society Of Australia Cambridge Core




Dik Ucgen 16 15 75 90 Ucgeni Temel Matematik Evde Egitim Matematik Felsefesi




Toward 1 Km Ensemble Forecasts Over Large Domains In Monthly Weather Review Volume 145 Issue 8 17




Dik Ve Ozel Ucgenler
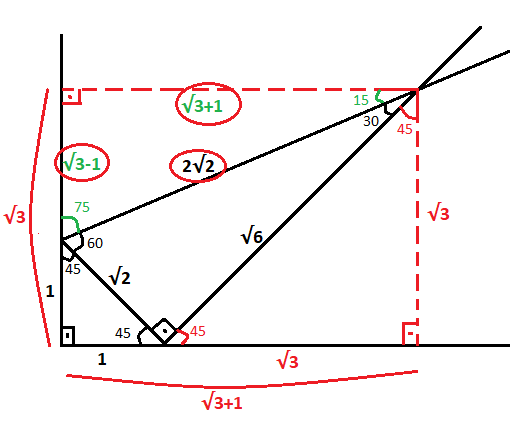



15 75 90 Ucgeni Kenarlari Arasindaki Oran Eksi Up




Dik Ucgen Konu Anlatimi Ve Ornek Soru Cozumu Kunduz




Matnℓsnye On Instagram Buyuk Hazine Serisine Bu Guzel Postla Guzel Bir Ara Tum Onemli Geometri Formuller Bir Arada L Geometri Kalkulus Harmanlanmis Ogrenme




Dik Ucgende Trigonometri Bikifi
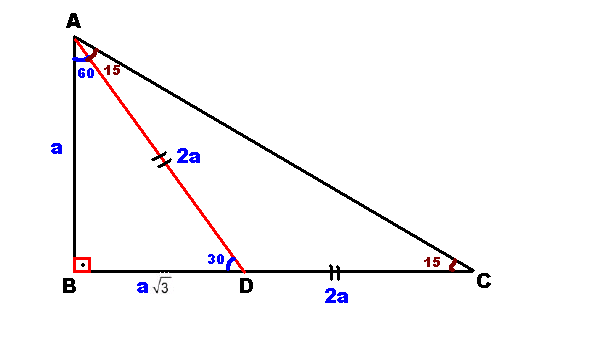



15 75 90 Ucgeni 2 3 Ispat




Effectiveness Of Non Pharmaceutical Interventions To Contain Covid 19 A Case Study Of The Spring Pandemic Wave In New York City Journal Of The Royal Society Interface




Are Gastrointestinal Symptoms Specific For Coronavirus 19 Infection A Prospective Case Control Study From The United States Gastroenterology
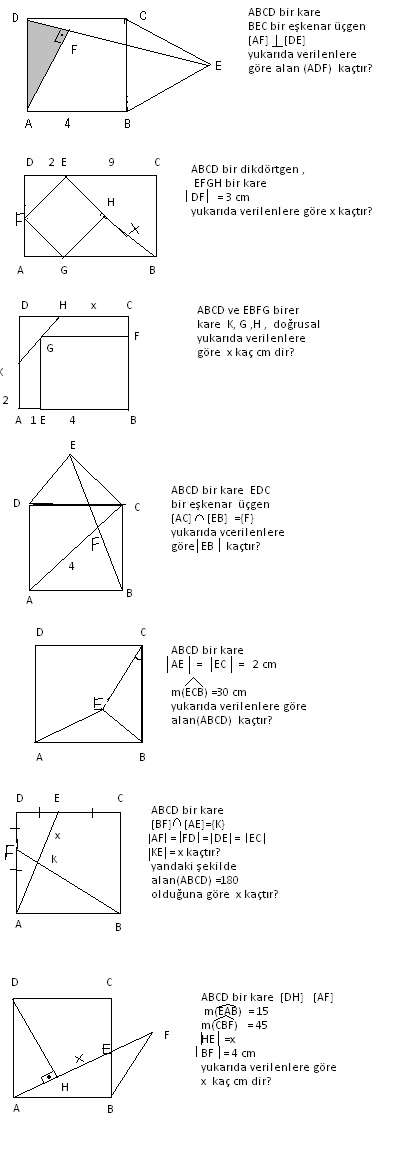



Kare Sorulari Lutfen Yardimci Olurmusunuz Acillll




Comparison Of Global Precipitation Estimates Across A Range Of Temporal And Spatial Scales In Journal Of Climate Volume 29 Issue 21 16




15 75 90 Ucgeni Ozelliklerinin Ispati Youtube




The Urban Crime And Heat Gradient In High And Low Poverty Areas Sciencedirect




15 75 90 Ucgeni Pow Bylge




15 75 90 Ucgeni Ucgende Acilar Ders Notlari Kunduz
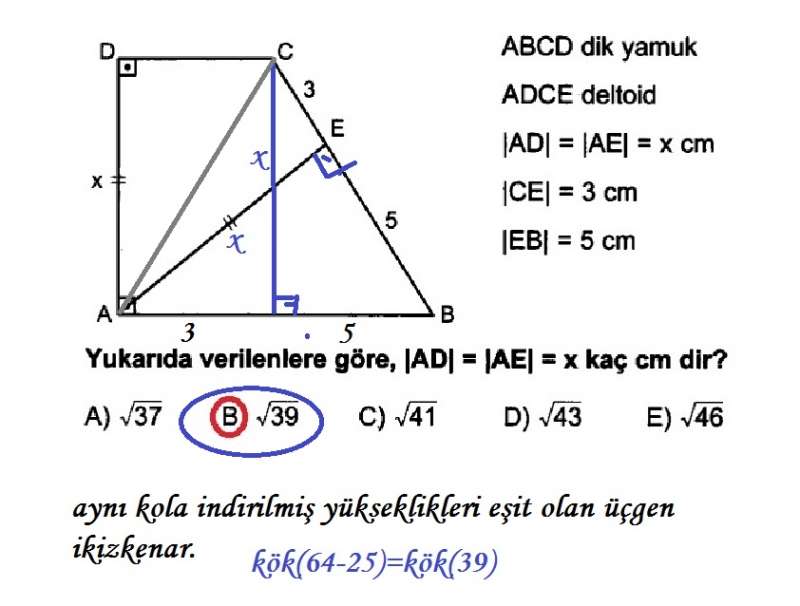



Yamuk




Non Canonical Metabolic Pathways In The Malaria Parasite Detected By Isotope Tracing Metabolomics Molecular Systems Biology




Long Term Population Dynamics Of Dreissenid Mussels Dreissena Polymorpha And D Rostriformis A Cross System Analysis Strayer 19 Ecosphere Wiley Online Library




15 75 90 Ozel Ucgeni Oluyor Ama Ben Sadece O Ucgenin Yukseklik Le Ilgili Ozelligini Biliyorum Baska Eodev Com



15 75 90 Ucgnler Sitem



What Are The Side Relationships Of A 15 75 90 Triangle Quora




15 75 90 Ucgeni Not Bu



Capsules R High Resolution Stock Photography And Images Page 2 Alamy



90 75 15 Ucgeni 90 75 15 Ucgeni Ozellikleri Ucgen Gen Tr



Dik Acili Ucgenin Kenar Ve Aci Ozellikleri Nedir




Dik Ucgen 16 15 75 90 Ucgeni Temel Matematik Evde Egitim Matematik Felsefesi
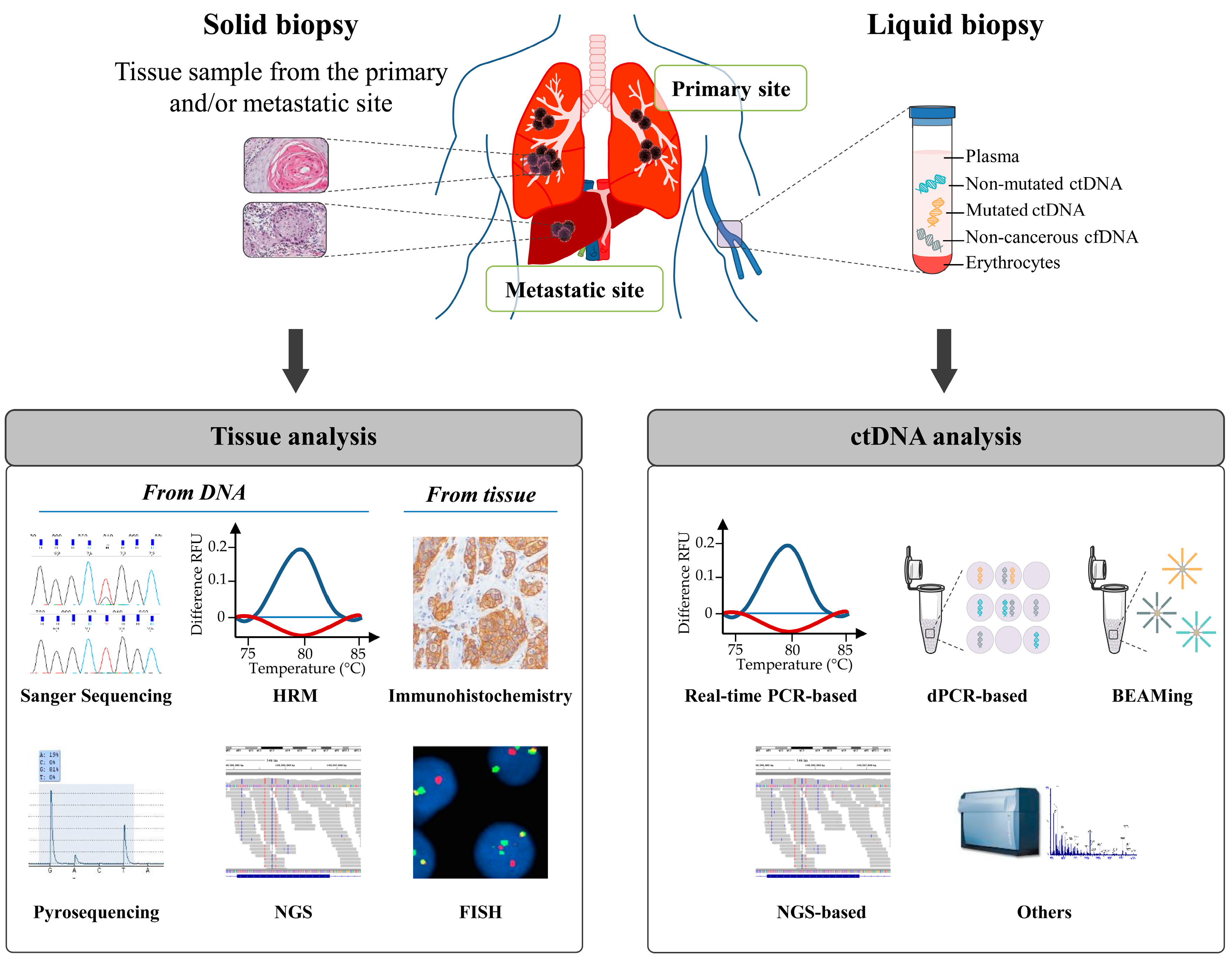



Ijms Free Full Text Circulating Cell Free Tumor Dna Detection As A Routine Tool Forlung Cancer Patient Management Html
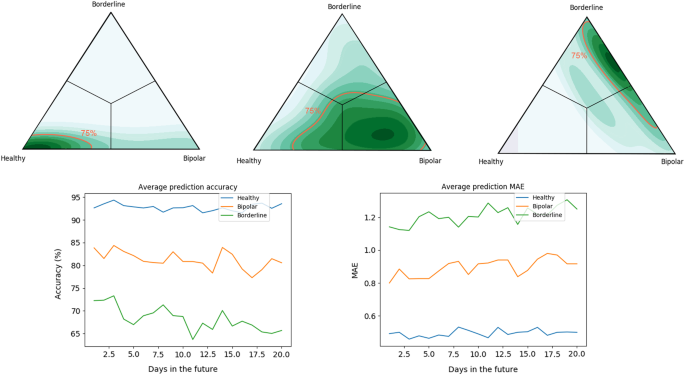



A Signature Based Machine Learning Model For Distinguishing Bipolar Disorder And Borderline Personality Disorder Translational Psychiatry




15 75 90 Ucgeni Kurali Nedir 15 75 90 Ozel Ucgeni Ozellikleri Ve Ornek Sorular Egitim Haberleri




Group Loyalty And The Taste For Redistribution Journal Of Political Economy Vol 109 No 3




Dershane Osym Lys Ygs Video Ders Konu Anlatim Izle On The App Store
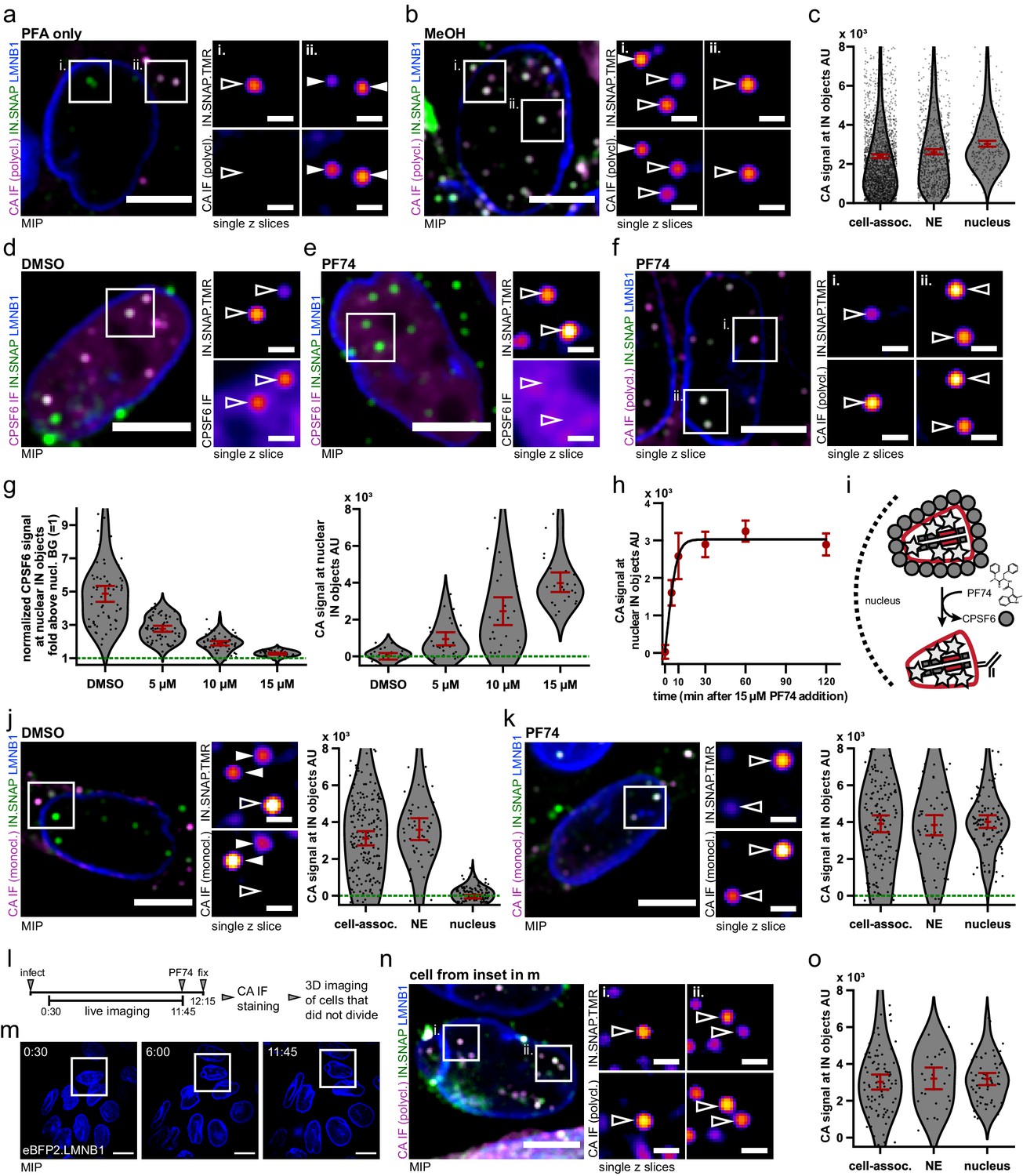



Hiv 1 Uncoating By Release Of Viral Cdna From Capsid Like Structures In The Nucleus Of Infected Cells Elife



15 75 90 Ucgeni




Geometri Sorularim 9 Adet
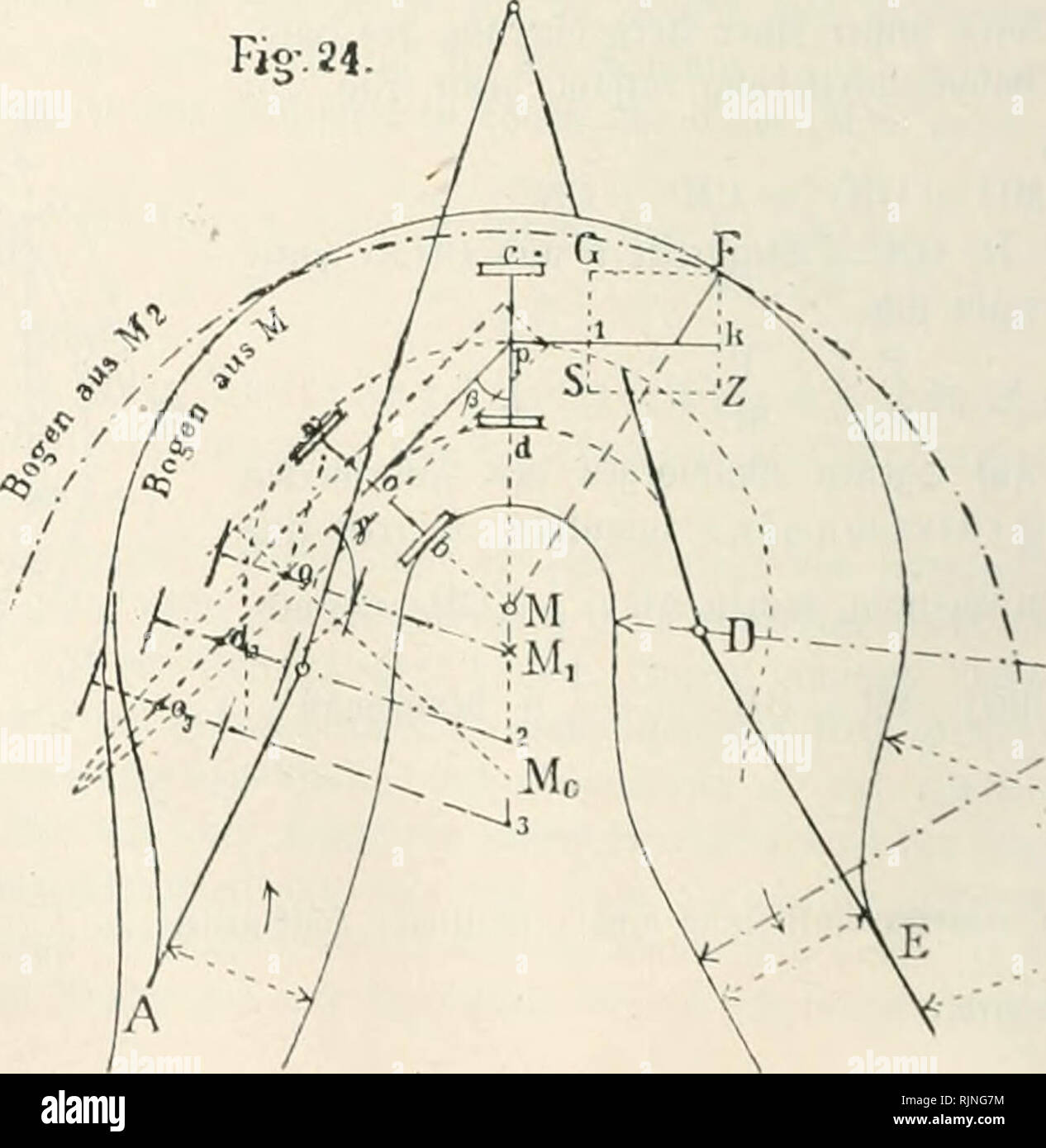



B 2 A F R 36 High Resolution Stock Photography And Images Alamy




15 75 90 Ucgeni Ozellikleri Ve Kurallari




Dik Ucgen Vikipedi




無料印刷可能15 75 90 Ucgeni Kenar Bagintilari




15 75 90 Ucgen Ozelligi Ve 5 Ornek Cozum Youtube



Dik Ucgen Vikipedi




Small Dense Low Density Lipoprotein Cholesterol Is The Most Atherogenic Lipoprotein Parameter In The Prospective Framingham Offspring Study Journal Of The American Heart Association




Acb Ucgen Alani Buldum Adc Ucgeni 15 75 90 Icin De Sadece Yerlestirmeyi Yapamadim Bakar Misinz Eodev Com



0 件のコメント:
コメントを投稿